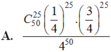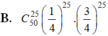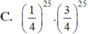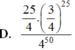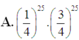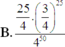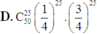Giả sử học sinh đó chọn x câu đúng (với \(0\le x\le10\)), như vậy sẽ có \(10-x\) câu sai
Số điểm học sinh đó đạt được là:
\(5x-2\left(10-x\right)=7x-20\)
Điểm dưới 1 \(\Rightarrow7x-20< 1\Rightarrow x< 3\)
Vậy học sinh đó trả lời đúng 0,1 hoặc 2 câu
Xác suất đúng khi chọn mỗi câu hỏi là 1/4 còn xác suất sai là 3/4 nên xác suất học sinh đó dưới 1 điểm là:
\(C_{10}^0.\left(\dfrac{1}{4}\right)^0.\left(\dfrac{3}{4}\right)^{10-0}+C_{10}^1.\left(\dfrac{1}{4}\right)^1.\left(\dfrac{3}{4}\right)^{10-1}+C_{10}^2.\left(\dfrac{1}{4}\right)^2.\left(\dfrac{3}{4}\right)^{10-2}=...\)