Cho hình hộp chữ nhật ABCD.A'B'C'D' Chứng tỏ
a) A'B' // mp (ABCD)
b) mp (CDD'C') vuông góc mp(ABCD)
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' . Chứng minh rằng :
a) BDD’B’ là hình chữ nhật
b ) B B ’ ⊥ m p ( A B C D ) c ) m p ( A B B ’ A ’ ) ⊥ m p ( A B C D )

a) BB’ ⊥ A’B’ (ABB’A’ là hình chữ nhật)
BB’ ⊥ B’C’ (BCC’B’ là hình chữ nhật)
=> BB’ ⊥ mp(A’B’C’D’)
=> BB’ ⊥ B’D’ hay
Hình bình hành BDD’B’ có một góc vuông nên là hình chữ nhật
BB’ vuông góc với hai đường thẳng cắt nhau AB và BC
=> BB’ ⊥ mp(ABCD)
c) mp(ABB’A’) chứa BB’ mà BB’⊥ mp(ABCD)
=> mp(ABB’A’) ⊥ mp(ABCD)
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' . Chứng minh rằng:
a ) B D / / B ’ D ’
b ) B B ’ / / m p ( C C ’ D ’ D ) , B ’ D ’ / / m p ( A B C D )
c ) m p ( A B B ’ A ’ ) / / m p ( D C C ’ D ’ )
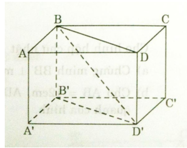
a) Ta có ABB’A’ là hình chữ nhật nên: AA’ // BB’ và AA’ = BB’
Tương tự ADD’A’ là hình chữ nhật:
AA’ // DD’ và AA’ = DD’
=> BB’ // DD’ và BB’ = DD’
Do đó BB’D’D là hình bình hành
=>BD // B’D’
b) BB’C’C là hình chữ nhật: BB’ // CC’ mà BB’ không thuộc mp(CC’D’D) và CC’ thuộc mp(CC’D’D) nên BB’ // mp(CC’D’D)
B’D’ // BD (cmt) mà B’D’ không thuộc mp (ABCD) và BD thuộc mp(ABCD) nên B’D’ // mp(ABCD)
c) Ta có: AB // CD (ABCD là hình chữ nhật)
AA’ // DD’ (ADD’A’ là hình chữ nhật)
Mà mp(ABB’A’) chứa hai đường thẳng cắt nhau AB và AA’ và mp(DCC’D’) chứa hai đường thẳng cắt nhau CD và DD’ => mp(ABB’A’) // mp(DCC’D’)
Cho hình hộp chữ nhật A B C D . A ' B ' C ' D ' . Chứng minh rằng:
a ) B D / / B ’ D ’
b ) B B ’ / / m p ( C C ’ D ’ D ) , B ’ D ’ / / m p ( A B C D )
c ) m p ( A B B ’ A ’ ) / / m p ( D C C ’ D ’ )
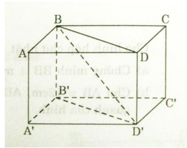
a) Ta có ABB’A’ là hình chữ nhật nên: AA’ // BB’ và AA’ = BB’
Tương tự ADD’A’ là hình chữ nhật:
AA’ // DD’ và AA’ = DD’
=> BB’ // DD’ và BB’ = DD’
Do đó BB’D’D là hình bình hành
=>BD // B’D’
b) BB’C’C là hình chữ nhật: BB’ // CC’ mà BB’ không thuộc mp(CC’D’D) và CC’ thuộc mp(CC’D’D) nên BB’ // mp(CC’D’D)
B’D’ // BD (cmt) mà B’D’ không thuộc mp (ABCD) và BD thuộc mp(ABCD) nên B’D’ // mp(ABCD)
c) Ta có: AB // CD (ABCD là hình chữ nhật)
AA’ // DD’ (ADD’A’ là hình chữ nhật)
Mà mp(ABB’A’) chứa hai đường thẳng cắt nhau AB và AA’ và mp(DCC’D’) chứa hai đường thẳng cắt nhau CD và DD’ => mp(ABB’A’) // mp(DCC’D’)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AC=a căn 3, BC = 2a, SA vuông góc (ABCD), SA=3a. Gọi O là giao điểm của AC và BD.
a) Cmr: CD vuông góc mp (SAD)
b) Cmr: (SAC) vuông góc mp (SBD)
c) Tính góc giữa SC v à mp (ABCD)
d) Tính góc giữa mp ( SAB) và mp (SBC).
e) Tính khoảng cách từ A đến mp ( SBD)
a: CD vuông góc AD; CD vuông góc SA
=>CD vuông góc (SAD)
b: BD vuông góc AC; BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
c: (SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=căn 3
=>góc SCA=60 độ
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AC=a căn 3, BC = 2a, SA vuông góc (ABCD), SA=3a. Gọi O là giao điểm của AC và BD. a) Cmr: CD vuông góc mp (SAD) b) Cmr: (SAC) vuông góc mp (SBD) c) Tính góc giữa SC v à mp (ABCD) d) Tính góc giữa mp ( SAB) và mp (SBC). e) Tính khoảng cách từ A đến mp ( SBD)
a: CD vuông góc AD; CD vuông góc SA
=>CD vuông góc (SAD)
b: BD vuông góc AC; BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AA' = a, AB = b, AD = c.
Tính bán kính của đường tròn là giao tuyến của mp(ABCD) với mặt cầu trên.
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, ∆ S A B đều cạnh a nằm trong mặt; phẳng vuông góc với mp(ABCD). Biết mp(SCD) tạo với mp(ABCD) môt góc bằng 30 0 . Tính thể tích V của khối chóp S.ACBD.
A. V = a 3 3 8
B. V = a 3 3 4
C. V = a 3 3 2
D. V = a 3 3 3
Cho chóp S.ABCD đáy là hình chữ nhật. SA vuông góc đáy, SA=a√5;AD=2AB=4a.
a, Chứng minh BC vuông góc với mp (SAB).
b, Tính (SB;(ABCD).
(SC;(ABCD).
(SD;ABCD).
a: BC vuông góc AB; BC vuông góc SA
=>BC vuông góc (SAB)
b: (BS;(BACD))=(BS;BA)=góc SBA
tan SBA=SA/AB=căn 5/2
=>góc SBA=48 độ
(SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=1
=>góc SCA=45 độ
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AC=a căn 3, BC = 2a, SA vuông góc (ABCD), SA=3a. Gọi O là giao điểm của AC và BD. a) Tính góc giữa mp ( SAB) và mp (SBC). b) Tính khoảng cách từ A đến mp ( SBD)
Tuy nhiên đề cho giá trị cạnh AC với BC bị sai. Cạnh huyền AC (\(a\sqrt{3}\)) sao lại có giá trị nhỏ hơn cạnh góc vuông BC (2a) nhỉ?