cho hàm, số y = ( \(\sqrt{5}-2\)) x2 . xét tính đồng biến , nghịch biến của hàm số
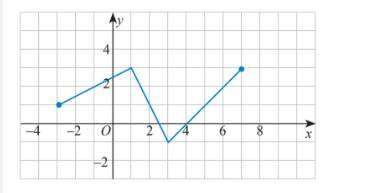
a) Tìm khoảng đồng biến và nghịch biến của hàm số có đồ thị sau:
b) Xét tính đồng biến, nghịch biến của hàm số \(y = f(x) = 5{x^2}\) trên khoảng (2; 5).
a) Từ đồ thị ta thấy hàm số xác định trên [-3;7]
+) Trên khoảng (-3; 1): đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (-3; 1).
+) Trên khoảng (1; 3): đồ thị có dạng đi xuống từ trái sang phải nên hàm số này nghịch biến trên khoảng (1; 3).
+) Trên khoảng (3; 7): đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (3; 7).
b) Xét hàm số \(y = 5{x^2}\) trên khoảng (2; 5).
Lấy \({x_1},{x_2} \in (2;5)\) là hai số tùy ý sao cho \({x_1} < {x_2}\).
Do \({x_1},{x_2} \in (2;5)\) và \({x_1} < {x_2}\) nên \(0 < {x_1} < {x_2}\), suy ra \({x_1}^2 < {x_2}^2\) hay \(5{x_1}^2 < 5{x_2}^2\)
Từ đây suy ra \(f({x_1}) < f({x_2})\)
Vậy hàm số đồng biến (tăng) trên khoảng (2; 5).
Cho hàm số y=\(\left(3-2\sqrt{2}\right)x+\sqrt{2}-1\)
a) Xét sự đồng biến và nghịch biến của các hàm số trên;
b) Tính giá trị của y khi x=\(3+2\sqrt{2}\)
a) Vì \(3-2\sqrt{2}>0\) nên hàm số đồng biến
b) Thay \(x=3+2\sqrt{2}\) vào hàm số, ta được:
\(y=\left(3-2\sqrt{2}\right)\left(3+2\sqrt{2}\right)+\sqrt{2}-1\)
\(=9-8+\sqrt{2}-1\)
\(=\sqrt{2}\)
a) `a=3-2\sqrt2>0 =>` Hàm số đồng biến.
b) `y=(3-2\sqrt2)(3+2\sqrt2)+\sqrt2-1=3^2-(2\sqrt2)^2+\sqrt2-1=\sqrt2`
`=> y=\sqrt2` khi `x=3+2\sqrt2`
Xét sự đồng biến, nghịch biến của hàm số: y = - x 3 + x 2 - 5
Tập xác định: D = R
y'= -3x2 + 2x
y' = 0 ⇔ -3x2 + 2x = 0 ⇔ x.(-3x + 2) = 0 ⇔ 
Bảng biến thiên:
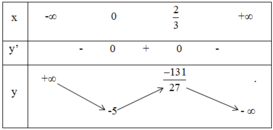
Vậy hàm số nghịch biến trong các khoảng (-∞ ; 0) và (2/3 ; + ∞), đồng biến trong khoảng (0 ; 2/3).
Xét tính đồng biến, nghịch biến của hàm số trên các khoảng tương ứng
y = x 2 + 10 x + 9 t r ê n ( - 5 ; + ∞ )
Xét sự đồng biến, nghịch biến của các hàm số: y = x 4 + 8 x 2 + 5
TXĐ: R
y′ = 4 x 3 + 16 = 4x( x 2 + 4)
y' = 0 ⇔ 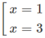
y' > 0 trên khoảng (0; + ∞ ) ⇒ y đồng biến trên khoảng (0; + ∞ )
y' < 0 trên khoảng (- ∞ ; 0) ⇒ y nghịch biến trên khoảng (- ∞ ; 0)
Xét tính đồng biến và nghịch biến của hàm số y = f x = - x 2 + 4 x - 2 trên các khoảng - ∞ ; 2 và 2 ; + ∞ .
A. f x đồng biến trên khoảng - ∞ ; 2 và nghịch biến trên khoảng 2 ; + ∞
B. f x đồng biến trên cả hai khoảng - ∞ ; 2 và 2 ; + ∞
C. f x nghịch biến trên khoảng - ∞ ; 2 và đồng biến trên khoảng 2 ; + ∞
D. f x nghịch biến trên cả hai khoảng - ∞ ; 2 và 2 ; + ∞
Với x 1 ≠ x 2 ta có:
f x 2 - f x 1 x 2 - x 1 = - x 2 2 + 4 x 2 - 2 - - x 1 2 + 4 x 1 - 2 x 2 - x 1 = - x 2 2 - x 1 2 + 4 ( x 2 - x 1 ) x 2 - x 1 = - x 2 + x 1 + 4 .
· Với x 1 , x 2 ∈ - ∞ ; 2 thì x1 < 2; x2 <2 nên x 1 + x 2 < 4 ⇒ - x 1 + x 2 + 4 > 0 nên f(x) đồng biến trên khoảng - ∞ ; 2 .
· · Với x 1 , x 2 ∈ 2 ; + ∞ thì x1>2; x2 >2 nên x 1 + x 2 > 4 ⇒ - x 1 + x 2 + 4 < 0 nên f(x) nghịch biến trên khoảng 2 ; + ∞ .
Vậy đáp án là A.
Nhận xét: Với 4 phương án trả lời cho ta biết f(x) đồng biến hoặc nghịch biến trên mỗi khoảng - ∞ ; 2 và 2 ; + ∞ .
Vì vậy, ta lấy hai giá trị bất kì x 1 < x 2 thuộc mỗi khoảng rồi so sánh f x 1 và f x 2 . Chẳng hạn x 1 = 0 ; x 2 = 1 có f 0 = - 2 ; f 1 = 1 nên f 0 < f 1 , suy ra f(x) đồng biến trên khoảng - ∞ ; 2 .
Trong các hàm số sau, hàm số nào là hàm số bậc nhất? Hãy xác định các hệ số a, b xét xem hàm số nào đồng biến? Hàm số nào nghịch biến? y = 5 – 2 x 2
Ta có: y = 5 – 2 x 2 không phải là hàm số bậc nhất
a/ cho hàm số: y=(-3m - 2)x2. Tìm m để hàm số nghịch biến khi x < 0
b/ cho hàm số: y=(m2 - 2m + 3)x2. Xác định tính biến thiên của hàm số
c/ cho hàm số: y=(2m + 3)x2. Tìm m để hàm số đồng biến khi x>0
a.
Hàm số nghịch biến khi \(x< 0\Rightarrow-3m-2>0\Rightarrow m< -\dfrac{2}{3}\)
b.
Do \(a=m^2-2m+3=\left(m-1\right)^2+2>0;\forall m\)
\(\Rightarrow\) Hàm đồng biến khi \(x>0\) và nghịch biến khi \(x< 0\)
c.
Hàm đồng biến khi \(x>0\Rightarrow2m+3>0\)
\(\Rightarrow m>-\dfrac{3}{2}\)
Xét sự đồng biến, nghịch biến của hàm số:
y = 4 + 3x – x2
Tập xác định : D = R
y' = 3 – 2x
y’ = 0 ⇔ 3 – 2x = 0 ⇔ x = 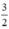
Ta có bảng biến thiên:
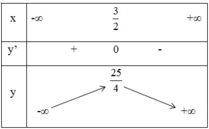
Vậy hàm số đồng biến trong khoảng (-∞; 3/2) và nghịch biến trong khoảng (3/2 ; + ∞).