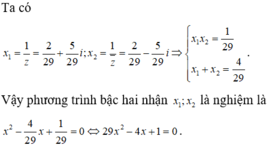Tìm phương trình bậc hai biết nó nhận các số 7 và −11 là nghiệm.

Những câu hỏi liên quan
Cho hai số 11 và 28. Tìm phương trình bậc nhất hai ẩn có hệ số của biến bậc cao nhất là 1 và nhận hai số trên là nghiệm.
Phương trình cần tìm là : x2 + x + = 0
gọi p và q là nghiệm của phương trình bậc hai 3x^2+7x+4=0 không giải phương trình hãy thành lập phương trình bậc hai với hệ số bằng số mà các nghiệm của nó là p/q-1 và q/p-1
Cho z = a + bi là một số phức. Hãy tìm phương trình bậc hai với hệ số thực nhận z và z làm nghiệm.
Cho 2 số 13 và 18. Tìm phương trình bậc nhất 2 ẩn có hệ số của biến bậc cao nhất là 1 và nhận hai hệ số trên là nghiệm.
\(\orbr{\begin{cases}x-\frac{13}{18}y=0\\x-\frac{18}{13}y=0\end{cases}}\)
Đúng 0
Bình luận (0)
Cho số phức
z
2
−
5
i
. Tìm phương trình bậc hai nhận
1
z
và
1
z
¯
làm nghiệm. A.
29
x
2
+
4
x
+
1
0
B.
29
x
2
+...
Đọc tiếp
Cho số phức z = 2 − 5 i . Tìm phương trình bậc hai nhận 1 z và 1 z ¯ làm nghiệm.
A. 29 x 2 + 4 x + 1 = 0
B. 29 x 2 + 4 x - 1 = 0
C. 29 x 2 - 4 x + 1 = 0
D. 29 x 2 - 4 x - 1 = 0
Cho số phức
z
2
-
5
i
. Tìm phương trình bậc hai nhận
1
z
và
1
z
làm nghiệm. A.
29
x
2
+
4
x
+
1
0
B.
29
x
2
+
4
x
-
1
0
C.
29...
Đọc tiếp
Cho số phức z = 2 - 5 i . Tìm phương trình bậc hai nhận 1 z và 1 z làm nghiệm.
A. 29 x 2 + 4 x + 1 = 0
B. 29 x 2 + 4 x - 1 = 0
C. 29 x 2 - 4 x + 1 = 0
D. 29 x 2 - 4 x - 1 = 0
Xác định phương trình bậc nhất hai ẩn nhận hai cặp số (1;2) và (2;5) là hai nghiệm
Gọi phương trình bậc nhất hai ẩn cần tìm là \(ax+by=0\)
Theo đề, ta có:
\(\left\{{}\begin{matrix}a+2b=0\\2a+5b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a+4b=0\\2a+5b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=0\\a=0\end{matrix}\right.\)
Đúng 1
Bình luận (1)
Một phương trình bậc hai một ẩn nếu có các hệ số a+b+c=0 thì nó có hai nghiệm là gì?
Thì chỉ có 2 nghiệm thôi bạn. Lúc đầu học là 2 nghiệm phân biệt nhưng trong 1 lần làm bài tập, ptrình có a + b + c = 0, mình kết luận có 2 nghiệm phân biệt nhưng kết quả tính có 2 nghiệm y hệt nhau. Hỏi thầy thì thầy nói để " 2 nghiệm " thôi, không có " phân biệt "
Đúng 0
Bình luận (0)
Cho phuong trình bậc hai ax2 + bx+ c =0 có hai nghiệm x1,x2 deu khác 0 . Phương trình bậc hai nhận 2x1 và 2x2 làm nghiệm là:
x1+x2=-b/a; x1x2=c/a
=>2x1+2x2=-2b/a; 4x1x2=4c/a
=>PT cần tìm là x^2+2b/a*x+4c/a=0
Đúng 0
Bình luận (0)