Cho hình bình hành ABCD. Gọi G là một điểm trên cạnh CD , K là một điểm trên cạnh CB sao cho DG/GC = 1/2 và BK/KC = 3/2. Gọi giao điểm của BD với AG và AK lần lượt là E và F. Tính độ dài các đoạn DE , EF , FB nếu biết BD = 24cm

Những câu hỏi liên quan
Cho hình bình hành ABCD. Gọi G là một điểm trên cạnh CD , K là một điểm trên cạnh CB sao cho DG/GC = 1/2 và BK/KC = 3/2. Gọi giao điểm của BD với AG và AK lần lượt là E và F. Tính độ dài các đoạn DE , EF , FB nếu biết BD = 24cm
Cho hình bình hành ABCD có điểm G thuộc cạnh CD sao cho D G = 1 4 D C . Gọi E là giao điểm của AG và BD. Tính tỉ số DE/DB
Cho hình bình hành \(ABCD\). Gọi \(I\) và \(K\) lần lượt là trung điểm của các cạnh \(AB\) và \(CD\); \(E\) và \(F\) lần lượt là giao điểm của \(AK\) và \(CI\) với \(BD\).
a) Chứng minh tứ giác \(AEFI\) là hình thang
b) Chứng minh \(DE = EF = FB\)
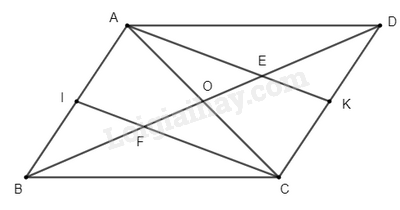
a) Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(AB\) // \(CD\), \(AD\) // \(BC\); \(AB = CD\); \(AD = BC\)
Mà \(IA = IB = \frac{{AB}}{2}\); \(KD = KC = \frac{{CD}}{2}\) (do \(I\),\(K\) là trung điểm)
Suy ra \(IA = IB = KD = KC\)
Xét tứ giác \(AKCI\) có:
\(AI = KC\) (cmt)
\(AI\) // \(KC\)
Suy ra \(AKCI\) là hình bình hành
Suy ra \(IC\) // \(AK\)
Hay \(IF\) // \(AE\)
Suy ra \(AEFI\) là hình thang
b) Vì \(ABCD\), \(AKCI\) là hình bình hành (gt)
Suy ra \(O\) là trung điểm của \(AC\), \(BD\), \(KI\)
Suy ra \(OD = OB = \frac{1}{2}BD\) (1)
Xét tam giác \(ADC\) có hai trung tuyến \(AK\), \(DO\) cắt nhau tại \(E\)
Suy ra \(E\) là trọng tâm của tam giác
Suy ra \(ED = \frac{2}{3}DO\) (2)
Chứng minh tương tự ta có \(BF = \frac{2}{3}BO\) (3)
Từ (1), (2), (3) suy ra \(ED = BF = \frac{1}{3}BD\)
Suy ra \({\rm{EF}} = \frac{1}{3}BD\)
Vậy \(DE = EF = FB\)
Đúng 0
Bình luận (0)
cho hình bình hành ABCD . Trên 2 cạnh AB và CD lần lượt lấy 2 điểm E và F sao cho AE = CF . Trên 2 cạnh AD và BC lần lượt lấy điểm H và G sao cho AH = CG .
a. Cmr EH = GF
b. Cmr tứ giác EHFG là hình bình hành
c. Gọi I là trung điểm của BD , Cmr 3 điểm E,I,F thẳng hàng
cho hình bình hành ABCD , điểm G thuộc cạnh CD sao cho DG=1/3 .Gọi E là gia của AG và BD. Tính DE/DB=?
Xem chi tiết
Bài 1: Cho hình bình hành ABCD. Trên 2 cạnh AB và CD lần lượt lấy các điểm E, F sao cho AE= CF. Gọi O là giao điểm của AC và BD. CMR: E và F đối xứng nhau qua O.
Cho hình bình hành ABCD. Trên cạnh AD, BC lần lượt lấy điểm H, G sao cho DH=BG a) Chứng minh: AGCH là hình bình hành. b) Gọi O là giao điểm của AC và BD. Chứng minh: G,O,H thẳng hàng c) Trên cạnh AB lấy điểm E, gọi F là giao điểm của EO với DC. Chứng minh:EGFH là hình bình hành
Cho hình bình hành ABCD. Trên cạnh AB và CD lần lượt lấy các điểm E; F sao cho AE = CF.
a)Chứng minh: AF = EC.
b)Gọi M là giao điểm của AF và DE, N là giao điểm của BF và CE. Chứng minh tứ giác EMFN là hình bình hành.
c) Ở phía ngoài của hình bình hành dựng 2 tam giác đều ADP và DCQ. Chứng minh rằng tam giác BPQ là tam giác đều.
Cho hình thang ABCD (AB//CD). Gọi E và F lần lượt là trung điểm của AC và BD.
a/ CMR:EF//AB//CD, EF=1/2(CD-AB)
b/ Gọi M,N,P,Q lần lượt là giao điểm các đường phân giác trong và phân giác ngoài góc A,B,C,D. Chứng minh các điểm E, F, M, N, P, Q nằm trên đường trung bình của hình thang ABCD
c/ Tính độ dài các đoạn MN và PQ theo độ dài các cạnh hình thang ABCD
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
Đúng 0
Bình luận (0)
bạn ấy muốn hỏi bài chứ bạn ấy không muốn xin nôi quy bạn ơi
Đúng 0
Bình luận (0)
















