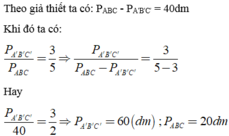`a) ΔA'B'C' ∼ ΔABC` theo tỉ lệ đồng dạng `k = 2/5`

`=> (A'B')/(AB) = (A'C')/(AC) = (B'C')/(BC) = 2/5`

Theo tính chất dãy tỉ số bằng nhau

`=> (A'B')/(AB) = (A'C')/(AC) = (B'C')/(BC) = (A'B' + A'C' + B'C')/(AB + AC + BC) = 2/5`

`=> (PΔA'B'C')/(PΔABC) = 2/5`

b) Từ a) ta có: `(PΔA'B'C')/(PΔABC) = 2/5`

`=> (PΔA'B'C')/2 = (PΔABC)/5`

Áp dụng tính chất dãy tỉ số bằng nhau:

`=>  (PΔA'B'C')/2 = (PΔABC)/5 = (PΔABC - PΔA'B'C')/(5-2) = 30/3 = 10`

`=> PΔA'B'C' = 10 xx 2 = 20 (cm)`

`PΔABC = 10 xx 5 = 50 (cm)`

@@@@

Em không bt đúng hay sai đúng thì tíc không đúng thì thôi . Em mong là đúng 

tam giác ABC có MN thuộc AB ; PQ thuộc AC ; Ab =12 ;AC=16; Am=3; AN=6 ; AP=2 ; AQ=4 thì 2 đường thẳng nào song song

HT

Lời giải:

a. $\triangle A'B'C'\sim \triangle ABC$ theo tỉ số $k$

$\Rightarrow \frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{A'C'}{AC}=k$

$\Rightarrow A'B'=kAB; B'C'=kBC; C'A'=kCA$

$\Rightarrow A'B'+B'C'+C'A'=k(AB+BC+AC)$

$\Rightarrow P_{A'B'C'}=kP_{ABC}$

$\Rightarrow \frac{P_{A'B'C'}}{P_{ABC}}=k$

b.

Chu vi tam giác ABC:

$40:(5-3).3=60$ (dm) 

Chu vi tam giác A'B'C':

$40:(5-3).5=100$ (dm)

Cho a',b',c' là số đo cạnh của tam giác A'B'C'
       a,b,c là số đo cạnh của tam giác ABC
a) Theo đề bài ta có: \(\frac{a'}{a}=\frac{b'}{b}=\frac{c'}{c}=k=\frac{3}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có: \(\frac{a'}{a}=\frac{b'}{b}=\frac{c'}{c}=\frac{a'+b'+c'}{a+b+c}=\frac{P_{A'B'C'}}{P_{ABC}}=k=\frac{3}{5}\)
Vậy tỉ số chu vi hai tam giác đã cho là 3/5
b) Chu vi tam giác ABC là: \(P_{ABC}=40:\left(5-3\right)\cdot5=100\left(dm\right)\)
Chu vi tam giác A'B'C' là:  \(P_{A'B'C'}=P_{ABC}-40dm=100dm-40dm=60\left(dm\right)\)

a, Gọi CV tam giác A'B'C' là P', ABC là P

\(\Delta A'B'C'~\Delta ABC\)theo tỉ số đồng dạng \(k=\frac{3}{5}\)

\(\Rightarrow\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}=\frac{3}{5}\)

Áp dụng t/c DTSBN , ta có  :

\(\frac{3}{5}=\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}\)

\(=\frac{A'B'+B'C'+C'A'}{AB+BC+CA}=\frac{P'}{P}\)

Vậy tỉ số chu vi tam giác A'B'C' và ABC là \(\frac{3}{5}\)

Câu a) hôm trước làm rồi , quên làm câu b) nên giờ làm tiếp (:

b) 

Ta có : \(\frac{P'}{P}=\frac{3}{5} \Rightarrow P'=\frac{3}{5}P\)

Ta lại có : P - P' = 40

\(\Rightarrow P-\frac{3}{5}P=40\)

\(\Rightarrow\frac{2}{5}P=40\)

\(\Rightarrow P=100\Leftrightarrow P'=60\)

Vậy chu vi tam giác ABC bằng 100dm và chu vi tam giác A’B’C’ là 60dm

a) Ta có \(\Delta ABC\backsim\Delta DEF\) theo tỉ số đồng dạng \(k = \frac{2}{5}\) nên

\(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = \frac{2}{5} \Rightarrow AB = \frac{2}{5}DE;AC = \frac{2}{5}DF;BC = \frac{2}{5}EF\).

Chu vi tam giác \(ABC\) là:

\({C_{ABC}} = AB + AC + BC\) (đơn vị độ dài).

Chu vi tam giác \(DEF\) là:

\({C_{DEF}} = DE + DF + EF\)

Tỉ số chu vi của \(\Delta ABC\) và \(\Delta DEF\) là:

\(\frac{{{C_{ABC}}}}{{{C_{DEF}}}} = \frac{{AB + AC + BC}}{{DE + DF + EF}} = \frac{{\frac{2}{5}DE + \frac{2}{5}DF + \frac{2}{5}EF}}{{DE + DF + EF}} = \frac{{\frac{2}{5}\left( {DE + DF + EF} \right)}}{{DE + DF + EF}} = \frac{2}{5}\).

b) Chu vi tam giác \(ABC\) là:

\(36:\left( {5 - 2} \right).2 = 24\left( {cm} \right)\)

Chu vi tam giác \(DEF\) là:

\(36:\left( {5 - 2} \right).5 = 60\left( {cm} \right)\)

Vậy chu vi tam giác \(ABC\) là 24cm; chu vi tam giác \(DEF\) là 60cm.

xdhxef

6.)

Khi 2 tam giác đồng dạng với nhau thì cạnh nhỏ nhất  của tam giác này sẽ tương ứng với cạnh nhỏ nhất của tam giác kia.

Theo đề:\(A'B'\)=4,5

Ta có:\(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}\)

    \(\Rightarrow\)\(\frac{4,5}{3}=\frac{B'C'}{5}=\frac{C'A'}{7}\)

   \(\Rightarrow\)\(B'C'=7,5cm,C'A'=10,5cm\)

Diện tích tam giác ABC=20,25cm²

ta có tỉ số chu vi bằng tỉ số đồng dạng