Cho tam giác abc cân tại a . trên đường thẳng bc lấy điểm d và e sao cho d nằm giữa b và c . c nằm giữa d và e
c/m: a) ad bé hơn Ac
b) ac bé hơn Ae
Những câu hỏi liên quan
Cho tam giác ABC cân tại A, hai điểm D,E nằm trên đường thẳng BC, d nằm giữa B và C , C nằm giữa D và E. chứng minh AD<AC<AE. ai giúp em với ạ
Xem chi tiết
góc ADB=góc DAC+góc ACD
=>góc ADB>góc ACD
=>góc ADB>góc ABD
=>AB>AD
Vì ΔABC cân tại A
nên góc ACB<90 độ
=>góc ACE>90 đô
=>AE>AC=AB
=>AD<AC<AE
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, hai điểm D,E nằm trên đường thẳng BC, d nằm giữa B và C , C nằm giữa D và E. chứng minh AD<AC<AE. ai giúp em với ạ
Xem chi tiết
góc ADB=góc DAC+góc ACD
=>góc ADB>góc ACD
=>góc ADB>góc ABD
=>AB>AD
Vì ΔABC cân tại A
nên góc ACB<90 độ
=>góc ACE>90 đô
=>AE>AC=AB
=>AD<AC<AE
Đúng 1
Bình luận (0)
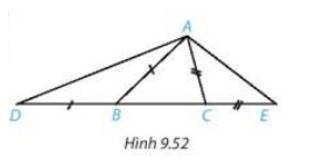
Cho tam giác ABC ( AB > AC). Trên đường thẳng chứa cạnh BC, lấy điểm D và điểm E sao cho B nằm giữa D và C, C nằm giữa B và E, BD = BA, CE = CA ( H.9.52)
a) So sánh \(\widehat {ADE}\) và \(\widehat {AED}\).
b) So sánh các đoạn thẳng AD và AE.
a)
\(AB > AC \Rightarrow \widehat {ABC} < \widehat {ACB}\)( quan hệ giữa góc và cạnh đối diện trong tam giác ABC)
\(\begin{array}{l} \Rightarrow {180^0} - \widehat {ABD} < {180^0} - \widehat {ACE}\\ \Rightarrow \widehat {ABD} > \widehat {ACE}\end{array}\)
Vì BD= BA nên tam giác ABD cân tại B \( \Rightarrow \widehat {ABD} = {180^0} - 2\widehat {ADB}\)
Vì CE = CA nên tam giác ACE cân tại C \( \Rightarrow \widehat {ACE} = {180^0} - 2\widehat {AEC}\)
\(\begin{array}{*{20}{l}}{ \Rightarrow {{180}^0} - 2\widehat {ADB} > {{180}^0} - 2\widehat {AEC}}\\{ \Rightarrow \widehat {ADB} < \widehat {AEC}}\\{Hay{\mkern 1mu} \widehat {ADE} < \widehat {AED}}\end{array}\)
b) Xét tam giác ADE ta có : \(\widehat {ADB} < \widehat {AEC}\)
\( \Rightarrow AD > AE\)(Quan hệ giữa cạnh và góc đối diện trong tam giác).
Đúng 0
Bình luận (0)
1) Cho góc xAy = 90 độ. Trên cạnh Ax lấy hai điểm B và D ( D nằm giữa A và B ) , trên cạnh Ay lấy hai điểm C và E ( C nằm giữa A và E ) sao cho AD = AC ; AB = AE
a) Chứng minh : tam giác ABC = tam giác AED ; tam giác BCE = tam giác EDB
b) Đường thẳng qua A vuông góc với BC tại H và cắt DE tại M. Chứng minh M là trung điểm của DE
Cho tam giác ABC vuông tại A có cạnh AB8cm, AC6cm. Trên cạnh AB lấy điểm D sao cho ADAC ( D nằm giữa A và B ). Trên tia đối của tia CA lấy điểm E sao cho AEAB ( C nằm giữa A và E ). Kẻ AH là đường cao của tam giác ABC. Đường thẳng AH cắt DE tại M ( M nằm giữa D và E )a) Tính độ dai cạnh BCb) Cm: tam giác ABCtam giác AEDc) Cm:AM là trung tuyến của tam giác ADEGiúp mk gải phần c) với nha. Mk sẽ tick cho.
Đọc tiếp
Cho tam giác ABC vuông tại A có cạnh AB=8cm, AC=6cm. Trên cạnh AB lấy điểm D sao cho AD=AC ( D nằm giữa A và B ). Trên tia đối của tia CA lấy điểm E sao cho AE=AB ( C nằm giữa A và E ). Kẻ AH là đường cao của tam giác ABC. Đường thẳng AH cắt DE tại M ( M nằm giữa D và E )
a) Tính độ dai cạnh BC
b) Cm: tam giác ABC=tam giác AED
c) Cm:AM là trung tuyến của tam giác ADE
Giúp mk gải phần c) với nha. Mk sẽ tick cho.
Cho tam giác ABC có góc A bé hơn 90 độ trên đường thẳng đi qua đỉnh A và vuông góc với AB lấy D sao cho AB=AD (C và D nằm khác phía đối với AB) trên đường thẳng đi qua A và vuông góc với AC lấy E sao cho AE=AC(B và E nằm khác phía đối với AC)
a) C/m BE=CD
b) C/m AB không vuông góc DE
cho tam giác ABC có góc A bé hơn \(90^0\)trên đường thẳng đi qua đỉnh A và vuông góc với AB lấy D sao cho AB=AD (C và D nằm khác phía đối AB),trên đường thẳng đi qua A và vuông góc với AC lấy E sao cho AE=AC(B và E nằm khác phía đối với AC)
a)C/m BE=CD
b) C/m AB không vuông góc DE
Cho t/g ABC vuông tại A có AB=4cm, Ac=3cm. Trên AB lấy D sao cho AD=AC (D nằm giữa A và B), trên tia đối của Ca lấy E sao cho AE=Ab (C nằm giữa A và E). Kẻ AH ⊥⊥Bc. Đoạn thẳng AH cắt DE tại M (M nằm giữa D và E)
a/ Tính BC
b/ CMR t/g ABC = t/g AED
c/ CMR t/g AMD cân tại M
*Nhớ vẽ hình nha!*
Cho tam giác ABC có góc A = 120 độ, đường phân giác AD (D thuộc BC). Vẽ DE vuông góc với AB, DF vuông góc với AC. a)tam giác DEF là tam giác gì?. b) Lấy K nằm giữa E và B, lấy I nằm giữa F và C sao cho EK = FI. Chứng minh tam giác DKI cân tại D. c) Từ C kẻ đường thẳng song song với AD cắt AB tại M. Chứng minh tam giác AMC đều. d) Tính DF biết AD = 4 cm
https://lazi.vn/edu/exercise/cho-tam-giac-abc-co-goc-a-120-do-duong-phan-giac-ad-d-thuoc-bc-ve-de-vuong-goc-voi-ab-df-vuong-goc
a) ΔAED=ΔAFDΔAED=ΔAFD(ch-gn)nên DE=DF.(hai cạnh tương ứng)
Mặt khác dễ dàng chứng minh được EDFˆ=60o
Vì vậy tam giác DEF là tam giác đều
b)ΔEDK=ΔFDT(hai cạnh góc vuông)
nen DK=DI(hai cạnh tương ứng).Do đó Tam giác DIK cân ở D
c) AD là tia phân giác của góc BAC nên DAB^=DAC^=1/2BAC^=60o
AD//MC(gt),do đó AMCˆ=DABˆ=60o(hai góc nằm trong vị trí đồng vị)
AMC^=CAD^=60o(hai góc nằm trong vị trí sole trong)
Tam giác AMC có hai góc bằng nhau và khoảng 60o nên là tam giác đều
d)Ta có AF=AC-FC=CM-FC=m-n.