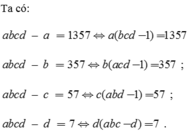
Nếu 1 trong a,b,c,d chẵn thì 1 trong 4 đẳng thức sai (kết quả ra chẵn do 1 số chẵn nhân 1 tích thì chẵn) =>a,b,c,d không tồn tại (do a,b,c,d phải thoả cả 4 đẳng thức) 
Nếu a,b,c,d đều lẻ thì 1số lẻ nhân cho 1 số chẵn (tích 3 số lẻ trừ 1 thì chẵn) thì là một số chẵn=>a,b,c,d không tồn tại 
Vậy không tồn tại các số nguyên a,b,c,d để thoả yêu cầu đề bài

Ta có góc A + B + C + D = 360⁰

Mà góc A = 6x, B = 5x + 8, C = 4x - 12, D = 3x + 4

=> 6x + 5x + 8 + 4x - 12 + 3x + 4 = 360⁰

=> 18x = 360⁰

=> x = 20⁰

Và thế x vào, ta có:

góc A = 120⁰

B = 108⁰

C = 68⁰

D = 64⁰ 

Do tổng 4 góc trong 1 tứ giác bằng 360 độ

\(\Rightarrow6x+\left(5x+8\right)+\left(4x-12\right)+\left(3x+4\right)=360\)

\(\Rightarrow18x=360\)

\(\Rightarrow x=20\)

Vậy: \(A=6x=120^0\)

\(B=5x+8=108^0\)

\(C=4x-12=68^0\)

\(D=3x+4=64^0\)

Xét tứ giác ABCD có

\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)(Định lí tổng bốn góc trong một tứ giác)

\(\Leftrightarrow6x+5x+8+4x-12+3x+4=360^0\)

\(\Leftrightarrow18x=360^0\)

hay \(x=20^0\)

Vậy: \(\widehat{A}=120^0;\widehat{B}=108^0;\widehat{C}=68^0;\widehat{D}=64^0\)

Ta chứng minh bất đẳng thức sau  

Với x, y, z > 0 ta luôn có  \(x^4+y^4+z^4\ge xyz\left(x+y+z\right)\)  (1)

Theo BĐT Cô-si

\(x^4+x^4+y^4+z^4\ge4\sqrt[4]{x^8y^4z^4}=4x^2yz\)

\(y^4+y^4+z^4+x^4\ge4\sqrt[4]{y^8z^4x^4}=4y^2zx\)

\(z^4+z^4+x^4+y^4\ge4\sqrt[4]{z^8x^4y^4}=4z^2xy\)

Cộng vế theo vế ta được:  \(4\left(x^4+y^4+z^4\right)\ge4\left(x^2yz+y^2zx+z^2xy\right)\)

\(\Leftrightarrow\)  \(x^4+y^4+z^4\ge xyz\left(x+y+z\right)\)

Vậy (1) đc c/m

Bất đẳng thức cần c/m có thể viết lại thành

\(\frac{abcd}{a^4+b^4+c^4+abcd}+\frac{abcd}{b^4+c^4+d^4+abcd}+\frac{abcd}{c^4+d^4+a^4+abcd}+\frac{abcd}{d^4+a^4+b^4+abcd}\le1\)

Áp dụng (1) ta có  

\(\frac{abcd}{a^4+b^4+c^4+abcd}\le\frac{abcd}{abc\left(a+b+c\right)+abcd}=\frac{abcd}{abc\left(a+b+c+d\right)}=\frac{d}{a+b+c+d}\)

Tương tự  

\(\frac{abcd}{b^4+c^4+d^4+abcd}\le\frac{a}{a+b+c+d}\)

\(\frac{abcd}{c^4+d^4+a^4+abcd}\le\frac{b}{a+b+c+d}\)

\(\frac{abcd}{d^4+a^4+b^4+abcd}\le\frac{c}{a+b+c+d}\)

Cộng theo vế suy ra đpcm.

Theo BĐT AM-GM: \(a^4+b^4\ge2a^2b^2\)

Tương tự suy ra \(a^4+b^4+c^4\)\(\ge a^2b^2+b^2c^2+c^2a^2\)

Tiếp tục dùng AM-GM: \(a^2b^2+b^2c^2=b^2\left(a^2+c^2\right)\ge2ab^2c\)

Tương tự suy ra \(a^2b^2+b^2c^2+c^2a^2\ge abc\left(a+b+c\right)\)

\(\Rightarrow a^4+b^4+c^4\ge abc\left(a+b+c\right)\)

\(\Rightarrow a^4+b^4+c^4+abcd\ge abc\left(a+b+c\right)+abcd\)\(=abc\left(a+b+c+d\right)\)

\(\Rightarrow\frac{1}{a^4+b^4+c^4+abcd}\le\frac{1}{abc\left(a+b+c+d\right)}\)

Tương tự cho 3 BĐT còn lại rồi cộng theo vế:

\(VT\le\frac{a+b+c+d}{abcd\left(a+b+c+d\right)}=\frac{1}{abcd}=VP\)

sorry nha!Mik ko bít làm.???

xong het de chua

biết làm phần a câu 2 đề 13 ko

khong co stn abcd nao thoa man