\(x^2+4y^2=x^2y^2-2xy\)

\(\Rightarrow x^2+4y^2+4xy=x^2y^2+2xy+1-1\)

\(\Rightarrow\left(x+2y\right)^2=\left(xy+1\right)^2-1\)

\(\Rightarrow\left(xy+1\right)^2-\left(x+2y\right)^2=1\)

\(\Rightarrow\left(xy-x-2y+1\right)\left(xy+x+2y+1\right)=1\)

Vì x,y là các số nguyên nên \(\left(xy-x-2y+1\right),\left(xy+x+2y+1\right)\) là các ước số của 1. Do đó ta có 2 trường hợp:

TH1: \(\left\{{}\begin{matrix}xy-x-2y+1=1\\xy+x+2y+1=1\left(1\right)\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}-xy+x+2y-1=-1\\xy+x+2y+1=1\end{matrix}\right.\)

\(\Rightarrow2\left(x+2y\right)=0\Rightarrow x=-2y\)

Thay vào (1) ta được:

\(-2y^2+1=1\Leftrightarrow y=0\Rightarrow x=0\)

TH2: \(\left\{{}\begin{matrix}xy-x-2y+1=-1\\xy+x+2y+1=-1\left(1\right)\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}-xy+x+2y-1=1\\xy+x+2y+1=-1\end{matrix}\right.\)

\(\Rightarrow2\left(x+2y\right)=0\Rightarrow x=-2y\)

Thay vào (1) ta được:

\(-2y^2+1=-1\Leftrightarrow\left[{}\begin{matrix}y=1\\y=-1\end{matrix}\right.\)

\(y=1\Rightarrow x=-2;y=-1\Rightarrow x=2\)

Vậy các cặp số nguyên (x;y) thỏa điều kiện ở đề bài là \(\left(0;0\right),\left(2;-1\right)\left(-2;1\right)\)

Ta có:

  x 2 +   102 =   y 2 ⇔ y 2 - x 2 = 102 N h ậ n   t h ấ y   h i ệ u   h a i   b ì n h   p h ư ơ n g   l à   m ộ t   s ố   c h ẵ n   N ê n   x , y   c ù n g   l à   s ố   c h ẵ n   h o ặ c   c ù n g   l à   s ố   l ẻ S u y   r a   y - x ;   y + x   l u ô n   l à   s ố   c h ẵ n   L ạ i   c ó   y 2 - x 2   =   102   ⇔ y - x y + x = 102 M à   y - x   v à   y + x   c ù n g   l à   s ố   c h ẵ n   S u y   r a   y - x y + x     c h i ế t   c h o   4   m à   102   k h ô n g   c h i a   h ế t   c h o   4   N ê n   k h ô n g   t ồ n   t ạ i   c ặ p   x ; y   t h ỏ a   m ã n   đ ề   b à i .                    

Đáp án cần chọn là :A

\(\Leftrightarrow\left(x-y\right)\left(x+y\right)=2017=1.2017\)

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-y=1\\x+y=2017\end{matrix}\right.\\\left\{{}\begin{matrix}x-y=-1\\x+y=-2017\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=1009\\y=1008\end{matrix}\right.\\\left\{{}\begin{matrix}x=-1009\\y=-1008\end{matrix}\right.\end{matrix}\right.\)

\(x^2+y^2+2\left(x+y\right)-xy=0\)

\(\Leftrightarrow4x^2-4xy+4y^2+8\left(x+y\right)=0\)

\(\Leftrightarrow\left(2x-y\right)^2+4\left(2x-y\right)+4+3y^2+12y+12=-16\)

\(\Leftrightarrow\left(2x-y+2\right)^2+3\left(y+2\right)^2=-16\)

Dễ thấy VT \(\ge0\) ; VP < 0 nên phương trình vô nghiệm 

\(x^2+y^2-2\left(x+y\right)=xy\)

\(\Rightarrow x^2-2x+1+y^2-2y+1=2+xy\)

\(\Rightarrow\left(x-1\right)^2+\left(y-1\right)^2=2+xy\)

Ta lại có : \(\left(x-1\right)^2+\left(y-1\right)^2\ge2\left(x-1\right)\left(y-1\right)\) (Bất đẳng thức Cauchy)

Tiếp tục phần tiếp theo

Dấu bằng xảy ra khi \(\left\{{}\begin{matrix}x=2\\y=2\end{matrix}\right.\)

\(\Rightarrow\left(x-1\right)^2+\left(y-1\right)^2=2+xy\) (vô lý vì 2=2+2.2)

⇒ Không có cặp (x;y) nguyên dương nào thỏa mãn đề bài

Đáp án A

Ta có, giả thiết  log x 2 + y 2 + 3 2 x + 2 y + 5 ≥ x 2 + y 2 + 3 ≤ 2 x + 2 y + 5 ⇔ x - 1 2 + y - 1 2 ≤ 4 là miền trong đường tròn tâm I(1;1) bán kính  R 1 = 2

Và x 2 + y 2 + 4 x + 6 y + 13 - m = 0 ⇔ x + 2 2 + y + 3 2 = m  là đường tròn tâm I(-2;-3); R 2 = m  

Khi đó, yêu cầu bài toán ⇔ R 1 + R 2 = I 1 I 2 ⇔ m + 2 = 5 ⇔ m = 9

Đáp án A

Ta có, giả thiết

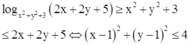
là miền trong đường tròn tâm I(1;1) bán kính R₁ = 2

Và 

\(\Leftrightarrow x^2-xy-5x+4y+9=0\)

\(\Leftrightarrow\left(x^2-xy\right)-\left(4x-4y\right)-x+9=0\)

\(\Leftrightarrow x\left(x-y\right)-4\left(x-y\right)-x+9=0\)

\(\Leftrightarrow\left(x-y\right)\left(x-4\right)-\left(x-4\right)+5=0\)

\(\Leftrightarrow\left(x-4\right)\left(x-y-1\right)=-5\)

Do \(x;y\in Z\Rightarrow\left(x-4\right);\left(x-y-1\right)\in Z\)

Ta có các trường hợp sau

+ TH1:

\(\left\{{}\begin{matrix}x-4=1\\x-y-1=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=9\end{matrix}\right.\)

+ TH2:

\(\left\{{}\begin{matrix}x-4=-1\\x-y-1=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=-3\end{matrix}\right.\)

+ TH3:

\(\left\{{}\begin{matrix}x-4=5\\x-y-1=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=9\\y=9\end{matrix}\right.\)

+ TH4:

\(\left\{{}\begin{matrix}x-4=-5\\x-y-1=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-3\end{matrix}\right.\)