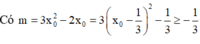cho đường thẳng (d):y=mx+2.giá trị của m để đường thẳng d tiếp xúc với đường kính bán kính 1.

Những câu hỏi liên quan
Trên mặt phẳng tọa độ Oxy, cho đường thẳng (d): y = mx - 1 (m ≠ 0). Tìm m để đường thẳng (d) tiếp xúc với đường tròn có tâm tại gốc tọa độ O và bán kính R = \(\dfrac{1}{\sqrt{10}}\)
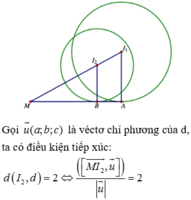
Trong không gian Oxyz, cho mặt cầu (S1) có tâm I1(2;1;0), bán kính R1 3; mặt cầu (S2) có tâm I2(0;1;0), bán kính R2 2. Đường thẳng d thay đổi nhưng luôn tiếp xúc với cả hai mặt cầu (S1),(S2). Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của khoảng cách từ điểm A(1;1;1) đến đường thẳng d. Giá trị của M.m bằng A.5,5 B. 4,5 C. 6,5 D. 7,5
Đọc tiếp
Trong không gian Oxyz, cho mặt cầu (S1) có tâm I1(2;1;0), bán kính R1 = 3; mặt cầu (S2) có tâm I2(0;1;0), bán kính R2 = 2. Đường thẳng d thay đổi nhưng luôn tiếp xúc với cả hai mặt cầu (S1),(S2). Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của khoảng cách từ điểm A(1;1;1) đến đường thẳng d. Giá trị của M.m bằng
A.5,5
B. 4,5
C. 6,5
D. 7,5
Cho đường tròn có tâm và góc tọa độ O bán kính 1 và đường thẳng (d) có phương trình 3x-4y=m^2-m+3
a) Xác định m để đường thẳng tiếp xúc vs đường tròn
b) Khoảng cách từ O đến đường thẳng có giá trị nhỏ nhất là bao nhiêu?
cho parabol (P): \(y=\dfrac{1}{4}x^{2}\) và đường thẳng (d): y=mx+n. Tìm giá trị của m,n để (d) đi qua điểm A(-1;-2) và tiếp xúc với (P)
Lời giải:
Để $(d)$ đi qua $A(-1;-2)$ thì: $-2=-m+n(1)$
Để $(d)$ và $(P)$ tiếp xúc nhau thì PT hoành độ giao điểm:
$\frac{1}{4}x^2-mx-n=0$ có nghiệm duy nhất
Điều này xảy ra khi:
$\Delta=m^2+n=0(2)$
Từ $(1);(2)\Rightarrow m=1$ hoặc $m=-2$
Nếu $m=1$ thì $n=-1$
Nếu $m=-2$ thì $n=-4$
Vậy............
Đúng 1
Bình luận (0)
cho đường tròn có tâm là gốc tọa độ bán kính 2√2 và đường thẳng (d):y+m^2+2=x.với m<0 để đường thẳng (d) tiếp xúc với đường tròn thì m bẳng bao nhiêu
Trong mặt phẳng Oxy cho đường thẳng (d) :\(y=\sqrt{m^2+1}.x-\sqrt{m^2+2}\), với m là tham số . CMR khi m thay đổi thì đường thẳng (d) luôn tiếp xúc với 1 đường tròn cố định . Xác định tâm và bán kính của đường tròn đó .
cho đường tròn có tâm là gốc tọa độ bán kính \(2\sqrt{2}\) và đường thẳng \(\left(d\right):y+m^2+2=x\).với m<0 để đường thẳng (d) tiếp xúc với đường tròn thì m bẳng bao nhiêu
Cho đồ thị
(
C
)
:
y
x
3
-
x
2
+
1
và đường thẳng (d): ymx. Tìm giá trị nhỏ nhất của m để
∆
tiếp xúc (C) và
∆
// d.
Đọc tiếp
Cho đồ thị ( C ) : y = x 3 - x 2 + 1 và đường thẳng (d): y=mx. Tìm giá trị nhỏ nhất của m để ∆ tiếp xúc (C) và ∆ // d.
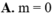
![]()
![]()
![]()
cho hàm số \(y=\left(m-1\right)x+2m-3\)(m là tham số ) có đồ thị là đường thẳng (d) . Tìm m để đường thẳng (d) tiếp xúc với đường tròn tâm O ( O là gốc tọa độ Oxy) bán kính 2 cm ( đơn vị trên 2 trục cm )

Vậy \(m=\frac{5}{4}\)thỏa mãn điều kiện đề bài