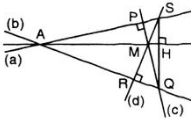
Cho điểm A nằm ngoài đường thẳng a qua A và song song với d Vẽ đường thẳng b qua A và cắt d tại H

Những câu hỏi liên quan
Cho (O;R) và điểm A nằm ngoài đường tròn (O). Qua A vẽ tiếp tuyến AB tiếp xúc với đường tròn (O) tại B. Vẽ một đường thẳng qua A cắt đường tròn tại hai điểm M và N ( M nằm giữa A và N). Qua M kẻ đường thẳng song song với AB cắt BN tại E. Gọi I là trung điểm của ME. Vẽ dây BQ của đường tròn (O) sao cho BQ đi qua điểm Ia) Chứng minh hai tam giác BMI và tam giác BQM đồng dạngb)Chứng minh tứ giác QIEN nội tiếpc) Chứng minh BM.QNBN.MQ
Đọc tiếp
Cho (O;R) và điểm A nằm ngoài đường tròn (O). Qua A vẽ tiếp tuyến AB tiếp xúc với đường tròn (O) tại B. Vẽ một đường thẳng qua A cắt đường tròn tại hai điểm M và N ( M nằm giữa A và N). Qua M kẻ đường thẳng song song với AB cắt BN tại E. Gọi I là trung điểm của ME. Vẽ dây BQ của đường tròn (O) sao cho BQ đi qua điểm I
a) Chứng minh hai tam giác BMI và tam giác BQM đồng dạng
b)Chứng minh tứ giác QIEN nội tiếp
c) Chứng minh BM.QN=BN.MQ
Bài 1: Vẽ đường thẳng a và đường thẳng b sao cho a song song với b.Lấy điểm M nằm ngoài 2 đường thẳng a,b vẽ đường thẳng cđi qua M và vuông góc với a và b.Bài 2:Cho góc xOy và điểm M nằm trong góc đó qua M kẻ MA vuông góc với Ox cắt Oy tại C, kẻ MB vuông góc với Oy cắt Ox tại D.Từ D và C kẻ các tia vuông góc với Ox;Oy các tia này cắt Ox;Oy lần lượt tại E,F và cắt nhau tại N.Tìm các cặp góc có các cạnh tương ứng song song.
Đọc tiếp
Bài 1: Vẽ đường thẳng a và đường thẳng b sao cho a song song với b.Lấy điểm M nằm ngoài 2 đường thẳng a,b vẽ đường thẳng cđi qua M và vuông góc với a và b.
Bài 2:Cho góc xOy và điểm M nằm trong góc đó qua M kẻ MA vuông góc với Ox cắt Oy tại C, kẻ MB vuông góc với Oy cắt Ox tại D.Từ D và C kẻ các tia vuông góc với Ox;Oy các tia này cắt Ox;Oy lần lượt tại E,F và cắt nhau tại N.Tìm các cặp góc có các cạnh tương ứng song song.
Trong các câu sau, câu nào đúng, câu nào sai?a) Qua điểm A nằm ngoài đường thẳng d, chỉ có một đường thẳng song song với d.b) Qua điểm A nằm ngoài đường thẳng d, có vô số đường thẳng song song với d.c) Nếu hai đường thẳng AB và AC cùng song song với đường thẳng a thì hai đường thẳng AB và AC trùng nhau.d) Nếu qua điểm A có hai đường thẳng cùng song song với đường thẳng d thì hai đường thẳng đó song song với nhau
Đọc tiếp
Trong các câu sau, câu nào đúng, câu nào sai?
a) Qua điểm A nằm ngoài đường thẳng d, chỉ có một đường thẳng song song với d.
b) Qua điểm A nằm ngoài đường thẳng d, có vô số đường thẳng song song với d.
c) Nếu hai đường thẳng AB và AC cùng song song với đường thẳng a thì hai đường thẳng AB và AC trùng nhau.
d) Nếu qua điểm A có hai đường thẳng cùng song song với đường thẳng d thì hai đường thẳng đó song song với nhau
Vẽ hình theo cách diễn đạt sau:a) Cho góc xOy60°.M là trung điểm bất kì nằm trong góc xOy. Vẽ MA vuông góc với Ox(A€Ox),AB vuông góc với Oy(B€Oy).Vẽ đường thẳng d đi qua M và song song với Oyb) Vẽ góc AOB60°Lấy điểm M nằm trong góc AOB. qua M vẽ, đường thẳng m song song với OA, cắt OB tại C và đường thẳng n song song OB cắt OA tại Dc) Vẽ tam giác ABC. Vẽ đường thẳng d1 đi qua B và vuông góc với AB. Vẽ đường thẳng d2 đi qua C và song song với AB. Gọi D là giao điểm của d1 và d2d) cho ba điểm A B...
Đọc tiếp
Vẽ hình theo cách diễn đạt sau:
a) Cho góc xOy=60°.M là trung điểm bất kì nằm trong góc xOy. Vẽ MA vuông góc với Ox(A€Ox),AB vuông góc với Oy(B€Oy).Vẽ đường thẳng d đi qua M và song song với Oy
b) Vẽ góc AOB=60°Lấy điểm M nằm trong góc AOB. qua M vẽ, đường thẳng m song song với OA, cắt OB tại C và đường thẳng n song song OB cắt OA tại D
c) Vẽ tam giác ABC. Vẽ đường thẳng d1 đi qua B và vuông góc với AB. Vẽ đường thẳng d2 đi qua C và song song với AB. Gọi D là giao điểm của d1 và d2
d) cho ba điểm A B, C bất kì.Hãy vẽ các đường trung trực của các đoạn thẳng AB, BC, CA
a
b
c
d
ĐÃ VẼ LẠI 2 LẦN.LẦN NÀY LÀ LẦN 3
=> CUỘC ĐỜI ĐEN NHỌ CỦA COOL KID :V
Đúng 1
Bình luận (0)
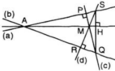
Cho hai đường thẳng phân biệt không song song a và b, điểm M nằm bên trong hai đường thẳng này. Qua M lần lượt vẽ đường thẳng c vuông góc với a tại P, cắt b tại Q và đường thẳng d vuông góc với b tại R, cắt a tại S. Chứng minh rằng đường thẳng qua M, vuông góc với SQ cũng đi qua giao điểm của a và b ?
(a) và (b) không song song nên (a) cắt (b), gọi giao điểm là O. Tam giác OSQ có PQ và RS là hai đường cao gặp nhau tại M nên M là trực tâm của tam giác nên đường thẳng vẽ từ M và vuông góc với SQ là đường cao thứ ba của tam giác tức là đường vuông góc với SQ vẽ từ M cũng đi qua giao điểm của a và b
Đúng 0
Bình luận (0)
(a) và (b) không song song nên (a) cắt (b), gọi giao điểm là O. Tam giác OSQ có PQ và RS là hai đường cao gặp nhau tại M nên M là trực tâm của tam giác nên đường thẳng vẽ từ M và vuông góc với SQ là đường cao thứ ba của tam giác tức là đường vuông góc với SQ vẽ từ M cũng đi qua giao điểm của a và b
Đúng 0
Bình luận (0)
Vì a và b không song song nên chúng cắt nhau giả sử tại A.
Xét ΔAQS có:
QP ⊥ AS (vì QP ⊥ a)
SR ⊥ AQ (vì SR ⊥ b)
Ta có QP và RS cắt nhau tại M. Vậy M là trực tâm của ΔAQS.
=> Đường thẳng đi qua M và vuông góc với QS tại H sẽ là đường cao thứ ba của ΔAQS.
Vậy MH phải đi qua đỉnh A của ΔAQS hay đường thẳng vuông góc với QS đi qua giao điểm của a và b (đpcm).
Đúng 0
Bình luận (0)
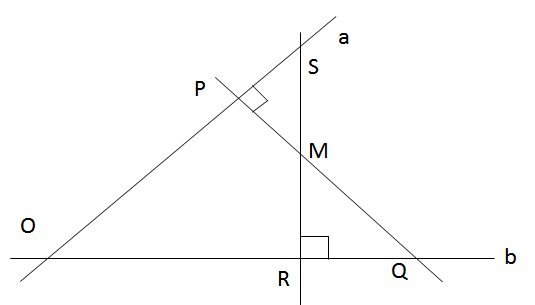
Cho hai đường thẳng phân biệt không song song a và b, điểm M nằm bên trong hai đường thẳng này. Qua M lần lượt vẽ đường thẳng c vuông góc với a tại P, cắt b tại Q và đường thẳng d vuông góc với b tại R, cắt a tại S. Chứng minh rằng đường thẳng qua M, vuông góc với SQ cũng đi qua giao điểm của a và b.
Gọi A là giao điểm của a và b.
Theo giả thiết c ⟘ a hay SR ⟘ AQ hay SR là đường cao của ΔASQ.
d ⟘ b hay PQ ⟘ AS hay QP là đường cao của ΔASQ.
SR cắt QP tại M ⇒ M là trực tâm của ΔASQ
⇒ AM ⟘ SQ
Vậy đường thẳng đi qua M và vuông góc với SQ cũng đi qua A (đpcm).
Đúng 0
Bình luận (0)
Cho hai đường thẳng phân biệt không song song a và b, điểm M nằm bên trong hai đường thẳng này. Qua M lần lượt vẽ đường thẳng c vuông góc với a tại P, cắt b tại Q và đường thẳng d vuông góc với b tại R, cắt a tại S. Chứng minh rằng đường thẳng qua M, vuông góc với SQ cũng đi qua giao điểm của a và b.
Chọn các câu khẳng định đúng:a) Qua điểm A nằm ngoài đường thẳng xy, có một đường thẳng song song với xy.b) Qua điểm A nằm ngoài đường thằng xy, có duy nhất một đường thẳng song song với xy.c) Qua điểm A nằm ngoài đường thẳng xy, có vô số đường thẳng song song với xy.d) Nếu hai đường thẳng AB và AC cùng song song với đường thẳng m thì hai đường thẳng AB và AC trùng nhau.e) Nếu qua điểm A có hai đường thẳng cùng song song với đường thẳng d thì hai đường thẳng đó song song với nhau
Đọc tiếp
Chọn các câu khẳng định đúng:
a) Qua điểm A nằm ngoài đường thẳng xy, có một đường thẳng song song với xy.
b) Qua điểm A nằm ngoài đường thằng xy, có duy nhất một đường thẳng song song với xy.
c) Qua điểm A nằm ngoài đường thẳng xy, có vô số đường thẳng song song với xy.
d) Nếu hai đường thẳng AB và AC cùng song song với đường thẳng m thì hai đường thẳng AB và AC trùng nhau.
e) Nếu qua điểm A có hai đường thẳng cùng song song với đường thẳng d thì hai đường thẳng đó song song với nhau
Chọn các câu khẳng định đúng:a) Qua điểm A nằm ngoài đường thẳng xy, có một đường thẳng song song với xy.b) Qua điểm A nằm ngoài đường thằng xy, có duy nhất một đường thẳng song song với xy.c) Qua điểm A nằm ngoài đường thẳng xy, có vô số đường thẳng song song với xy.d) Nếu hai đường thẳng AB và AC cùng song song với đường thẳng m thì hai đường thẳng AB và AC trùng nhau.e) Nếu qua điểm A có hai đường thẳng cùng song song vói đường thẳng d thì hai đường thẳng đó song song với nhau
Đọc tiếp
Chọn các câu khẳng định đúng:
a) Qua điểm A nằm ngoài đường thẳng xy, có một đường thẳng song song với xy.
b) Qua điểm A nằm ngoài đường thằng xy, có duy nhất một đường thẳng song song với xy.
c) Qua điểm A nằm ngoài đường thẳng xy, có vô số đường thẳng song song với xy.
d) Nếu hai đường thẳng AB và AC cùng song song với đường thẳng m thì hai đường thẳng AB và AC trùng nhau.
e) Nếu qua điểm A có hai đường thẳng cùng song song vói đường thẳng d thì hai đường thẳng đó song song với nhau