Những câu hỏi liên quan
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA; I, J, K, L lần lượt là trung điểm của các đoạn thẳng SM, SN, SP, SQ.
a) Chứng minh rằng bốn điểm I, J, K, L đồng phẳng và tứ giác IJKL là hình bình hành.
b) Chứng minh rằng IK//BC
c) Xác định giao tuyến của hai mặt phẳng (IJKL) và (SBC)
a) △ABC có M và N là trung điểm của AB, BC nên MN // AC (1)
△ACD có P và Q là trung điểm của CD, DA nên PQ // AC (2)
△SMN có I và J là trung điểm của SM, SN nên IJ // MN (3)
△SPQ có L và K là trung điểm của SQ, SP nên LK // PQ (4)
Từ (1)(2)(3)(4) suy ra IJ // LK. Do đó: I, J, K, L đồng phẳng.
Ta có: \(\dfrac{MN}{AC}=\dfrac{QP}{AC}=\dfrac{1}{2}\)
\(\dfrac{IJ}{MN}=\dfrac{LK}{PQ}=\dfrac{1}{2}\)
Từ (6)(7) suy ra: IJ = LK mà IJ // LK
Do đó: IJKL là hình bình hành.
b) Ta có: M, P lần lượt là trung điểm của AB, CD
Suy ra: MP // BC (1)
△SMP có: I, K là trung điểm của SM, SP
Suy ra: IK // MP (2)
Từ (1)(2) suy ra: IK // BC.
c) Ta có: J là điểm chung của hai mặt phẳng (IJKL) và (SBC)
Mà: IK // BC
Từ J kẻ Jx sao cho Jx // BC. Do đó, Jx là giao tuyến của hai mặt phẳng (IJKL) và (SBC).
Đúng 0
Bình luận (0)
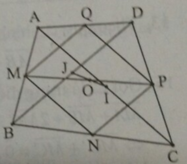
Cho tứ giác ABCD, gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. a) Chứng minh rằng MNPQ là hình bình hành b) Gọi I, J lần lượt là trung điểm của AC và BD. Chứng minh rằng các đoạn thẳng MP, QN, IJ đồng quy tại một điểm.
a: Xét ΔABD có
M là trung điểm của AB
Q là trung điểm của AD
Do đó: MQ là đường trung bình của ΔABD
Suy ra: MQ//BD và \(MQ=\dfrac{BD}{2}\left(1\right)\)
Xét ΔBCD có
P là trung điểm của CD
N là trung điểm của BC
Do đó: PN là đường trung bình của ΔABD
Suy ra: PN//BD và \(PN=\dfrac{BD}{2}\left(2\right)\)
Từ (1) và (2) suy ra MQ//PN và MQ=PN
hay MNPQ là hình bình hành
Đúng 0
Bình luận (0)
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Gọi O là giao điểm các đường chéo của tứ giác MNPQ, trung điểm các đoạn thẳng AC, BD tương ứng là I, J. Khẳng định nào sau đây đúng? A.
O
I
→
O
J
→
B.
O
A
→
...
Đọc tiếp
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Gọi O là giao điểm các đường chéo của tứ giác MNPQ, trung điểm các đoạn thẳng AC, BD tương ứng là I, J. Khẳng định nào sau đây đúng?
A. O I → = O J →
B. O A → = O C →
C. O B → = O D →
D. O I → = - O J →
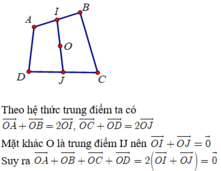
*Xét tam giác ABC có M; N là trung điểm của AB, BC nên MN là đường trung bình của tam giác.
⇒ M N / / A C ; M N = 1 2 A C ( 1 )
* Xét tam giác ADC có P; Q là trung điểm của CD, DA nên PQ là đường trung bình của tam giác.
⇒ P Q / / A C ; P Q = 1 2 A C ( 2 )
* Từ (1) (2) suy ra PQ// MN; PQ = MN. Do đó, tứ giác MNPQ là hình bình hành.
* Mà O là giao điểm của hình bình hành MNPQ nên O là trung điểm MP
* Xét tam giác ABC có MI là đường trung bình nên: M I / / B C ; M I = 1 2 B C ( 3 )
* Xét tam giác BCD có PJ là đường trung bình của các tam giác nên: P J / / B C ; P J = 1 2 B C ( 4 )
Từ (3) ( 4) suy ra ; tứ giác MIPJ là hình bình hành. Mà O là trung điểm MP nên điểm O là trung điểm của đoạn thẳng IJ. Từ đó ta có O I → = - O J →
Đáp án D
Đúng 0
Bình luận (0)
Cho tứ giác ABCD co AD = BC . Gọi I , J lần lượt là trung điểm của các cạnh AB và CD . H,K theo thứ tự lần lượt là trung điểm của 2 đường chéo AC và BD . CMR : IJ vuông góc với HK
Ta co:IA =IB(gt) ; HA =HC(gt)
Suy ra:HI la` đg tb của tam giac ABC
Suy ra:IH =1/2BC ;IH//BC (1)
Trong tam giac BDC co:KD =KB(gt) ;JD =JC(gt)
Suy ra :KJ la đg tb cu`a tam giac BDC
Suy ra :KJ =1/2BC ;KJ//BC (2)
Tu (1) va (2) suy ra :KJ = IH ;KJ // IH
Suy ra :tu giac KIHJ la hinh binh hanh(2 canh doi song song va bang nhau)(*)
Trong tam giac ADC co:HA =HC(gt) ;JD = JC(gt)
Suy ra :HJ la đg tb của tam giac ADC
Suy ra :HJ = 1/2AD
Mà AD =BC(gt) ; HI = 1/2BC(c/m tren)
Suy ra :HJ = HI (**)
Tu (*) va (**) suy ra tu giac KIHJ la hinh thoi (hbh co 2 canh ke bang nhau)
Suy ra :IJ vuong goc voi KH
Đúng 0
Bình luận (0)
Cho tứ giác ABCD. Gọi I, J lần lượt là trung điểm của AB và CD, O là trung điểm của IJ Mệnh đề nào sau đây đúng? A.
A
C
→
+
B
D
→
2
I
J
→
B.
A
C
→...
Đọc tiếp
Cho tứ giác ABCD. Gọi I, J lần lượt là trung điểm của AB và CD, O là trung điểm của IJ Mệnh đề nào sau đây đúng?
A. A C → + B D → = 2 I J →
B. A C → + B D → = I J →
C. A C → + B D → = 0 →
D. Tất cả sai
giúp e
Cho tứ giác ABCD co AD = BC . Gọi I , J lần lượt là trung điểm của các cạnh AB và CD . H,K theo thứ tự lần lượt là trung điểm của 2 đường chéo AC và BD . CMR : IJ vuông góc với HK
Cho tứ giác ABCD. Gọi I, J lần lượt là trung điểm của AB và CD, O là trung điểm của IJ . Tính vecto tổng
O
A
→
+
O
B
→
+
O
C
→
+
O
D
→
A. vecto AD B. Vecto BC C. Vecto DI D. Vecto 0
Đọc tiếp
Cho tứ giác ABCD. Gọi I, J lần lượt là trung điểm của AB và CD, O là trung điểm của IJ . Tính vecto tổng O A → + O B → + O C → + O D →
A. vecto AD
B. Vecto BC
C. Vecto DI
D. Vecto 0
cho tứ giác ABCD,gọi I,J lần lượt là trung điểm của AB và CD, O là trung điểm của IJ .chứng minh rằng: a)AC + BD 2IJ b) OA +OB +OC + OD 0 c) MA + MB +MC +MD4MO giúp em với ạ
Đọc tiếp
cho tứ giác ABCD,gọi I,J lần lượt là trung điểm của AB và CD, O là trung điểm của IJ .chứng minh rằng: a)AC + BD =2IJ b) OA +OB +OC + OD= 0 c) MA + MB +MC +MD=4MO giúp em với ạ
Cho tứ diện đều ABCD cạnh a. Gọi M, N lần lượt là trung điểm của CD và AB. Lấy
I
∈
A
C
,
J
∈
D
N
sao cho IJ // BM. Độ dài IJ theo a là A.
a
3
3
B.
a
2
3
C.
a...
Đọc tiếp
Cho tứ diện đều ABCD cạnh a. Gọi M, N lần lượt là trung điểm của CD và AB. Lấy I ∈ A C , J ∈ D N sao cho IJ // BM. Độ dài IJ theo a là
A. a 3 3
B. a 2 3
C. a 3 4
D. a 2 2