mô tả thuật toán sắp xếp chọn và thuật toán tìm kiếm tuần tự

Những câu hỏi liên quan
Em đã biết thiết kế một số thuật toán và chương trình: tìm kiếm tuần tự, tìm kiếm nhị phân, sắp xếp chèn, sắp xếp chọn, sắp xếp nổi bọt. Tất cả các thiết kế chương trình đó có điểm nào chung?
Theo em, để thiết kế một thuật toán đúng giải một bái toàn cho trước cần trải qua các bước như thế nào? Nêu quan điểm của riêng em và trao đổi với các bạn.
- Các thuật toán và chương trình mà em đã biết đều là các thuật toán cơ bản trong lập trình và giải quyết các vấn đề thông thường. Các điểm chung của chúng bao gồm: Tính đơn giản, độ phức tạp thấp.
- Theo em, để thiết kế một thuật toán đúng giải một bái toàn cho trước cần trải qua các bước:
1. Xác định bài toán
2. Tìm cấu trúc dữ liệu biểu diễn thuật toán.
3. Tìm Thuật Toán.
4. Lập Trình (Programming)
5. Kiểm thử chương trình (Testing program)
6. Tối ưu chương trình (optimization program)
Đúng 0
Bình luận (0)
Giả sử rằng mỗi phép tính đơn được thực hiện trong micro giây (1 us = một phần triệu giây). Hãy xác định giá trị lớn nhất của n trong các thuật toán tìm kiếm tuần tự, sắp xếp chèn và sắp xếp chọn nếu thời gian thực thi các thuật toán là 1 giây, 1 phút và 1 giờ?
1.Thuật toán tìm kiếm tuần tự:
- Độ phức tạp thời gian của thuật toán tìm kiếm tuần tự là O(n)
- Giá trị lớn nhất của n với thời gian thực thi là 1 giây: n = 1 giây * (106 us / phép tính) = 106
- Giá trị lớn nhất của n với thời gian thực thi là 1 phút: n = 1 phút * (60 giây / phút) * (106us / phép tính) = 6 * 107
- Giá trị lớn nhất của n với thời gian thực thi là 1 giờ: n = 1 giờ * (60 phút / giờ) * (60 giây / phút) * (106us / phép tính) = 3.6 * 109
2.Thuật toán sắp xếp chèn:
- Độ phức tạp thời gian của thuật toán sắp xếp chèn là O(102
- Giá trị lớn nhất của n với thời gian thực thi là 1 giây: n = sqrt(1 giây * (106us / phép tính)) =103
- Giá trị lớn nhất của n với thời gian thực thi là 1 phút: n = sqrt(1 phút * (60 giây / phút) * (106us / phép tính)) = 6 * 104
- Giá trị lớn nhất của n với thời gian thực thi là 1 giờ: n = sqrt(1 giờ * (60 phút / giờ) * (60 giây / phút) * (106us / phép tính)) = 3.6 * 106
3. Thuật toán sắp xếp chọn:
- Độ phức tạp thời gian của thuật toán sắp xếp chọn là O(n2)
- Giá trị lớn nhất của n là: n = sqrt(1 giây * (106us / phép tính)) = 1000.
Thời gian thực thi là 1 phút:
Giá trị lớn nhất của n là: n = sqrt(1 phút * (60 giây / phút) * (106us / phép tính)) = 60000.
Thời gian thực thi là 1 giờ:
Giá trị lớn nhất của n là: n = sqrt(1 giờ * (60 phút / giờ) * (60 giây / phút) * (106us / phép tính)) = 3.6 * 106
Đúng 1
Bình luận (0)
Cho trước một đây số đã được sắp xếp theo thứ tự tăng dần. Hãy đọc, quan sát và thảo luận cách làm sau đây để hiểu được thuật toán tìm kiếm nhị phân, biết được tính ưu việt của thuật toán này so với thuật toán tìm kiếm tuần tự trên một dây các phần từ đã sắp xếp.
Thuật toán tìm kiếm nhị phân thực hiện tìm kiếm một mảng đã sắp xếp bằng cách liên tục chia các khoảng tìm kiếm thành 1 nửa. Bắt đầu với một khoảng từ phần tử đầu mảng, tới cuối mảng. Nếu giá trị của phần tử cần tìm nhỏ hơn giá trị của phần từ nằm ở giữa khoảng thì thu hẹp phạm vi tìm kiếm từ đầu mảng tới giửa mảng và nguợc lại. Cứ thế tiếp tục chia phạm vi thành các nửa cho dến khi tìm thấy hoặc đã duyệt hết.
Thuật toán tìm kiếm nhị phân tỏ ra tối ưu hơn so với tìm kiếm tuyết tính ở các mảng có độ dài lớn và đã được sắp xếp. Ngược lại, tìm kiếm tuyến tính sẽ tỏ ra hiệu quả hơn khi triển khai trên các mảng nhỏ và chưa được sắp xếp.
Đúng 0
Bình luận (0)
Quan sát cách thực hiện thuật toán tìm kiếm tuần tự trên ví dụ cụ thể sau. Hãy trao đổi thảo luận để hiểu và mô tả được thuật toán trong trường hợp tổng quát.
Thuật toán tìm kiếm tuần tự: Duyệt lần lượt các phần tử của dãy để tìm phần tử có giá trị bằng K. Nếu tìm thấy, trả về chỉ số của phản tử bằng K; Ngược lại, thông báo không tìm thây và trả về giá trị -1. Thuật toán có thê duyệt từ đâu dãy hoặc từ cuối dãy.
Đúng 0
Bình luận (0)
Theo em, với dãy đã sắp thứ tự và cho một số x cụ thể
a) Trường hợp nào tìm kiếm tuần tự nhanh hơn tìm kiếm nhị phân?
b) Về trung bình thuật toán tìm kiếm tuần tự hay thuật toán tìm kiếm nhị phân tốt hơn?
a. Ví dụ một bài toán tìm kiếm trong thực tế: Giáo viên muốn tìm tên bạn Chung trong danh sách lớp sau:

Các bước thực hiện thuật toán tìm kiếm nhị phân cho bài toán trên:
- Bước 1: Xét vị trí ở giữa dãy, đó là vị trí số 5
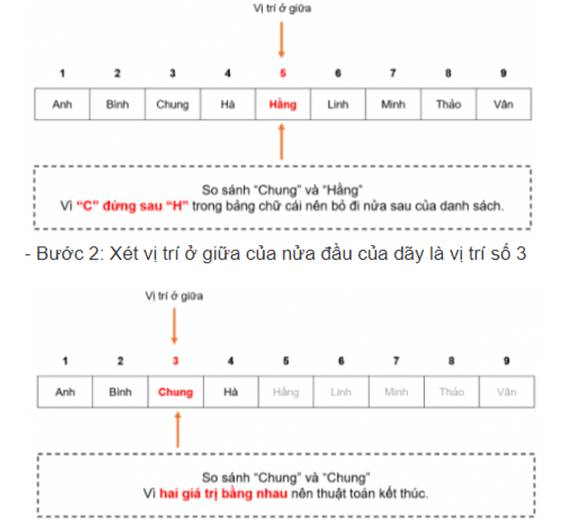
- Vì sau bước 2 đã tìm thấy tên học sinh nên thuật toán kết thúc.
b) Thuật toán tìm kiếm nhị phân
- Thuật toán tìm kiếm nhị phân thu hẹp được phạm vi tìm kiếm chỉ còn tối đa là một nửa sau mỗi lần lặp. Thuật toán chia bài toán thành những bài toán nhỏ hơn giúp tăng hiệu quả tìm kiếm.
Thuật toán tuần tự
- Mô tả thuật toán phải cụ thể, rõ ràng, đầy đủ, đầu vào là gì, đầu ra là gì và chỉ rõ sự kết thúc thuật toán.
- Cần mô tả thuật toán cho tốt thì người máy hay máy tính mới hiểu đúng và thực hiện được.
- Nếu không, kết quả thực hiện thuật toán có thể không như mong đợi.
Đúng 0
Bình luận (0)
Mô phỏng thuật toán tìm kiếm tuần tự với dãy B: 1 - 5 - 7 - 6 với k = 7
Mô phỏng thuật toán tìm kiếm tuần tự với dãy B: 1 - 5 - 7 - 6 với k = 9
Làm ơn trình bày giúp mik nha
#include <bits/stdc++.h>
using namespace std;
long long x,i,n,k;
int main()
{
cin>>n>>k;
for (i=1; i<=n; i++)
{
cout<<x;
if (x==k) cout<<i<<" ";
}
return 0;
}
Đúng 0
Bình luận (0)
Quan sát chương trình mô tả thuật toán sắp xếp chèn. Hãy thảo luận và đưa ra các lập luận để kiểm tra tính đúng của thuật toán sắp xếp chèn.
Tính đúng của thuật toán cần được chứng minh bằng lập luận toán học. Sử dụng các bộ dữ liệu kiểm thử có thể làm tăng độ tin cậy của chương trình nhưng chưa chứng minh được tính đúng của thuật toán.
Đúng 0
Bình luận (0)
Mô phỏng thuật toán tìm kiếm tuần tự với bộ dữ liệu: n = 10; k = 21;
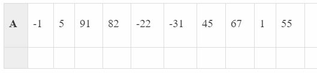
Mô phỏng thuật toán
| A | -1 | 5 | 91 | 82 | -22 | -31 | 45 | 67 | 1 | 55 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Kết quả: Dãy A không có số hạng có giá trị bằng k = 21
Đúng 0
Bình luận (0)
mô tả thuật toán và viết chương trình sắp xếp dãy số A gồm N phần tử(N được nhập từ bàn phím) sắp xếp theo thứ tự tăng dần
(pascal)













