a.m+2>n+2

Ta có: m >n

=>m+2 > n+2 (cộng hai vế với 2)

do đó m+2>n+2

b, -2m < -2n

Ta có: m > n

=> -2m < -2n (nhân hai vế với -2)

do đó -2m<-2n

c,2m-5>2n-5

Ta có: m>n

=>2m>2n (nhân hai vế với 2)

=>2m-5>2n-5 ( cộng hai vế với -5)

do đó 2m-5>2n-5

d,4-3m<4-3n

Ta có :m>n

=> -3m<-3n (nhân hai vế với -3)

=> 4-3m<4-3n (cộng 2 vế với 4)

bài 1:

a) 4n+4+3n-6<19

<=> 7n-2<19

<=> 7n<21 <=> n< 3

b) n\(^2\) - 6n + 9 - n\(^2\) + 16\(\leq\)43

-6n+25\(\leq\)43

-6n\(\leq\)18

n\(\geq\)-3

câu c

\(\Leftrightarrow\dfrac{2m-3}{2m+3}+\dfrac{2m+3}{2m-3}< 0\Leftrightarrow\dfrac{\left(2m-3\right)\left(2m-3\right)}{\left(2m+3\right)\left(2m-3\right)}+\dfrac{\left(2m+3\right)\left(2m+3\right)}{\left(2m-3\right)\left(2m+3\right)}< 0\)

\(\Leftrightarrow\dfrac{\left(2m-3\right)^2+\left(2m+3\right)^2}{\left(2m+3\right)\left(2m-3\right)}< 0\)

có

\(\left(2m-3\right)^2+\left(2m+3\right)^2>0\forall m\)

\(\Rightarrow\left(2m+3\right)\left(2m-3\right)< 0\Leftrightarrow\dfrac{-3}{2}< m< \dfrac{3}{2}\)

$3m-2m=1$ thì $m=1$. Còn $n$ ở đâu bạn?

a) Để y là hàm số bậc nhất

\(thì\Rightarrow\left\{{}\begin{matrix}\left(3m-1\right)\left(2n+3\right)=0\\4n+3\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}3m-1=0\\2n+3=0\end{matrix}\right.\\4n\ne-3\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}m=\dfrac{1}{3}\\n=-\dfrac{3}{2}\end{matrix}\right.\)

Vậy để y là hàm số bậc nhất thì \(m=\dfrac{1}{3}\) hoặc \(n=-\dfrac{3}{2}\)

b;c Tương tự.

Chọn đáp án C.

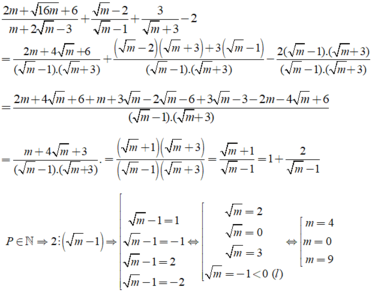
Thử lại, với m= 4 thì P =3 ( thỏa mãn)

Với m = 0 thì P = -1 ( không là số tự nhiên).

Với m = 9 thì P = 2 ( thỏa mãn)

Vậy m = 4 hoặc m = 9.

a)m>n công vế vs 2

=> m+2>n+2

b)  nhân cả 2 vế m>n cói -2, vì -2 là âm nên dấu bdt đổi chiều: -2m<-2n

c)m>n

=> 2m>2n

=> 2m-5>2n-5

d) m>n

=> -3m<-3n

=>4-3m<4-3n

a) Ta có: m > n => m + 2 > n + 2 (cộng hai vế với 2)
b) Ta có: m > n => -2m < -2n ( nhân hai vế với -2 và đổi chiều BĐT)
c) Ta có: m > n => 2m > 2n => 2m – 5 > 2n – 5
(nhân hai vế với 2, rồi cùng cộng vào hai vế với -5)
d) Ta có m > n => -3m < -3n ⇒ 4 – 3m < 4 – 3n
(nhân hai vế với -3 và đổi chiều BĐT, rồi cùng cộng vào hai vế với 4)