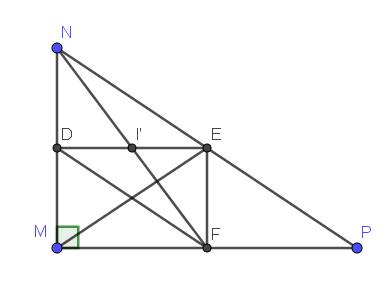
Cho tam giác mnp nhọn. Gọi d,e,f lầ lượt là trung điểm của mn,mp,np. H là giao điểm của mf và de. a) chứng minh h là trung điểm của mf b) chứng minh h là trung điểm của de. c) tứ giác mdef là hình gì. Vì sao d) tam giác mnp cần điều kiện gì thì tứ giác mdfe là hình chữ nhật.? Hình vuông?
MÌNH ĐANG CẦN GẤP NGÀY MAI MIK THI RỒI