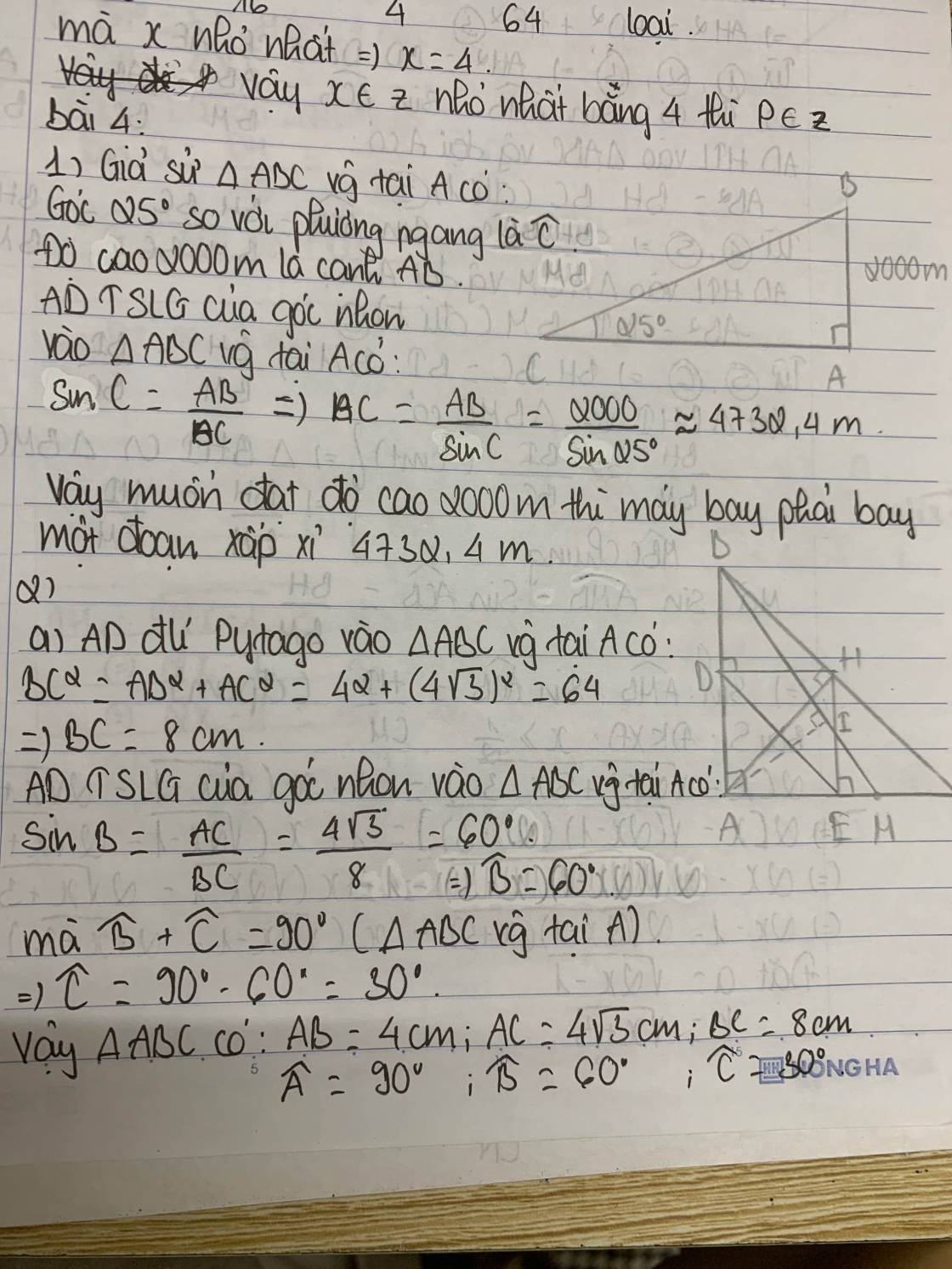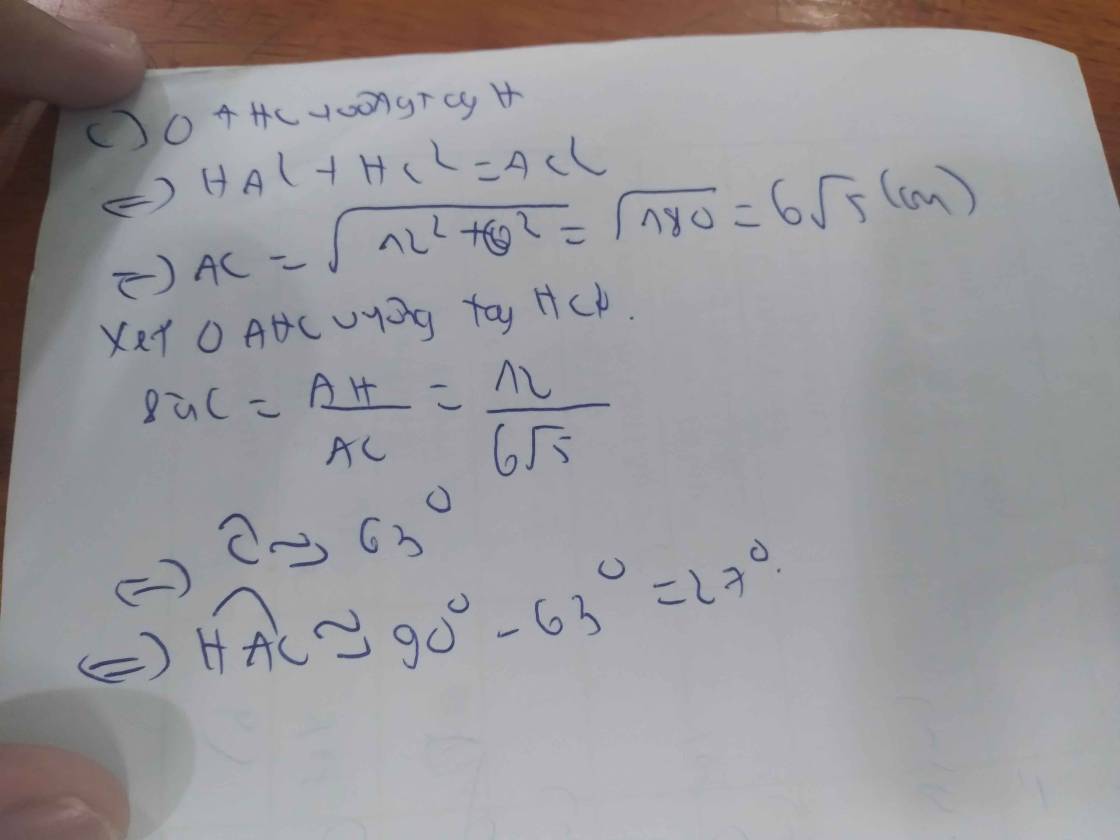(4 điểm) Cho tam giác $A B C$ vuông tại $A$, đường cao $A H(H \in B C)$.
a) Biết $A B=12 \mathrm{~cm}, B C=20 \mathrm{~cm}$, Tính $A C, A H$ và $\widehat{A B C}$ ( làm tròn đến độ);
b) Kẻ $H M$ vuông góc với $A B$ tại $M, H N$ vuông góc với $A C$ tại $N$. Chứng minh: $A N . A C=A C^2-H C^2$
c) Chứng minh: $A H=M N$ và $A M \cdot M B+A N \cdot N C=A H^2$;
d) Chứng minh: $\tan ^3 C=\dfrac{B M}{C N}$.

Những câu hỏi liên quan
Cho đường tròn $(O ; 2 \mathrm{~cm})$ đường kính $A B$. Lấy điểm $C$ trên đường tròn sao cho $ \widehat{AO C}=45^{\circ}$. Đường thẳng qua $C$ và vuông góc với $A B$ cắt $(O)$ tại $D$. Kéo dài $B C$ và $D A$ cắt nhau tại $M$. Kẻ $M H \perp A B$ tại $H$
a) Chứng minh tứ giác $A H M C$ nội tiếp.
b) Chứng minh $\widehat{A C H}=\widehat{A B C}$
c) Tính diện tích hình quạt $O C B$
Bài làm :
a) Ta có :
\(\widehat{ACB}\text{ là góc nội tếp chắn nửa đường tròn}\)
\(\Rightarrow\widehat{ACB}=90^o\Rightarrow\widehat{ACM}=180^o-\widehat{ACB}=90^o\)
Từ đó ; ta có :
\(\widehat{ACM}+\widehat{AHM}=90+90=180^o\)
=> Tứ giác AHMC là tứ giác nội tiếp đường tròn vì có 2 góc đối diện = 180 độ
=> Điều phải chứng minh
b) Theo phần a : Tứ giác AHMC là tứ giác nội tiếp
\(\Rightarrow\widehat{AMH}=\widehat{ACH}\left(1\right)\)
Xét đường tròn (O) : Góc ADC và góc ABC đều là 2 góc nội tiếp cùng chắn cung AC
\(\Rightarrow\widehat{ADC}=\widehat{ABC}\left(2\right)\)
Vì CD⊥AB ; MH⊥AB
=> CD//MH
=>∠ADC = ∠AMH ( 2góc so le trong ) (3)
Từ (1) ; (2) ; (3)
\(\Rightarrow\widehat{ABC}=\widehat{ACH}\)
=> Điều phải chứng minh
c)∠AOC = 45o
=>∠COB = 180 - 45 = 135o
\(\Rightarrow S_{OCB}=\frac{\pi.R^2.n}{360}=\frac{\pi.2^2.135}{360}=\frac{3}{2}\pi\left(cm^2\right)\)
a) Xét tứ giác AHMC có
góc ACM + góc AHM = 180 độ
Vậy tứ giác AHMC nội tiếp
Xem thêm câu trả lời
1) Một chiếc máy bay cất cánh theo một góc $25^{circ}$ so với phương ngang. Hỏi muốn đạt độ cao $2000 mathrm{~m}$ thì máy bay phải bay một đoạn đường là bao nhiêu mét? (làm tròn kết quả đến chũ số thâp phân thứ nhất).
2) Cho tam giác $A B C$ vuông tại $A$, đường cao $A H$.
a)Biết $A B4 mathrm{~cm}, A C4 sqrt{3} mathrm{~cm}$. Giải tam giác $A B C$.
b)Kẻ $H D, H E$ lần lượt vuông góc với $A B, A C$ ( $D$ thuộc $A B, E$ thuộc $A C$ ). Chứng minh $B D cdot D A+C E cdot E AA H^2$.
c)Lấy điểm $M$ nằm...
Đọc tiếp
1) Một chiếc máy bay cất cánh theo một góc $25^{\circ}$ so với phương ngang. Hỏi muốn đạt độ cao $2000 \mathrm{~m}$ thì máy bay phải bay một đoạn đường là bao nhiêu mét? (làm tròn kết quả đến chũ số thâp phân thứ nhất).
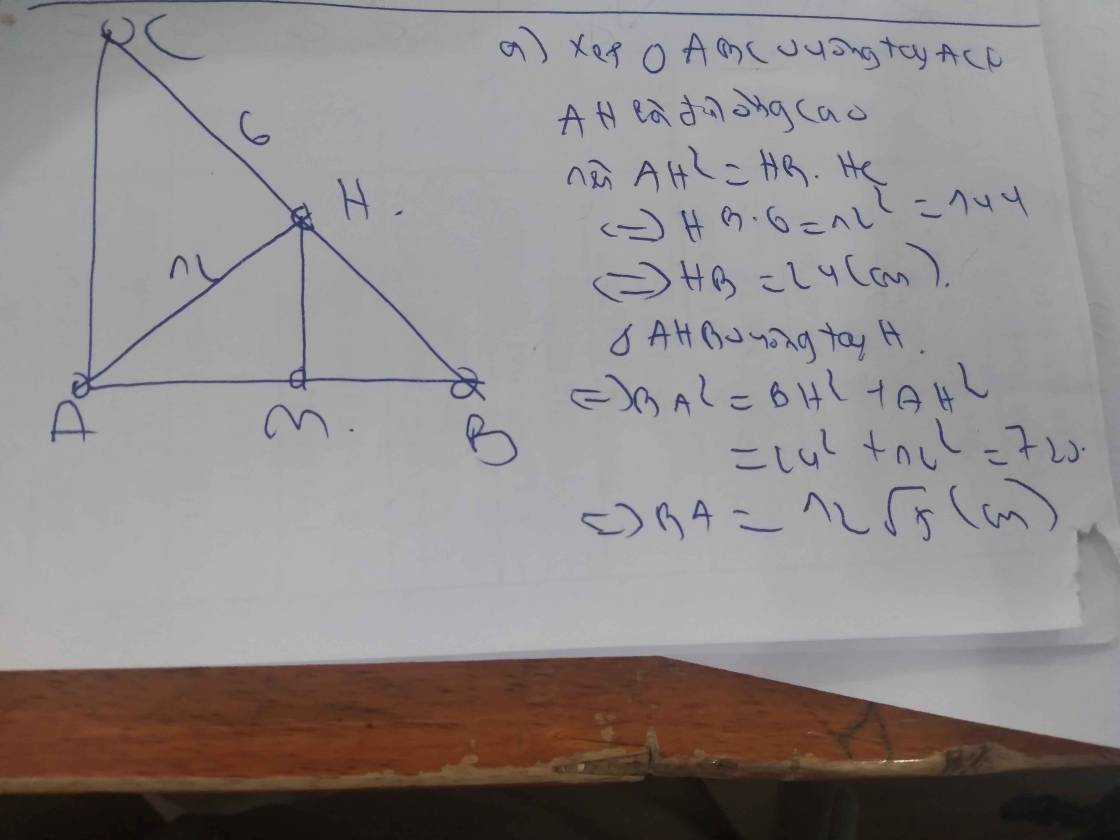
2) Cho tam giác $A B C$ vuông tại $A$, đường cao $A H$.
a)Biết $A B=4 \mathrm{~cm}, A C=4 \sqrt{3} \mathrm{~cm}$. Giải tam giác $A B C$.
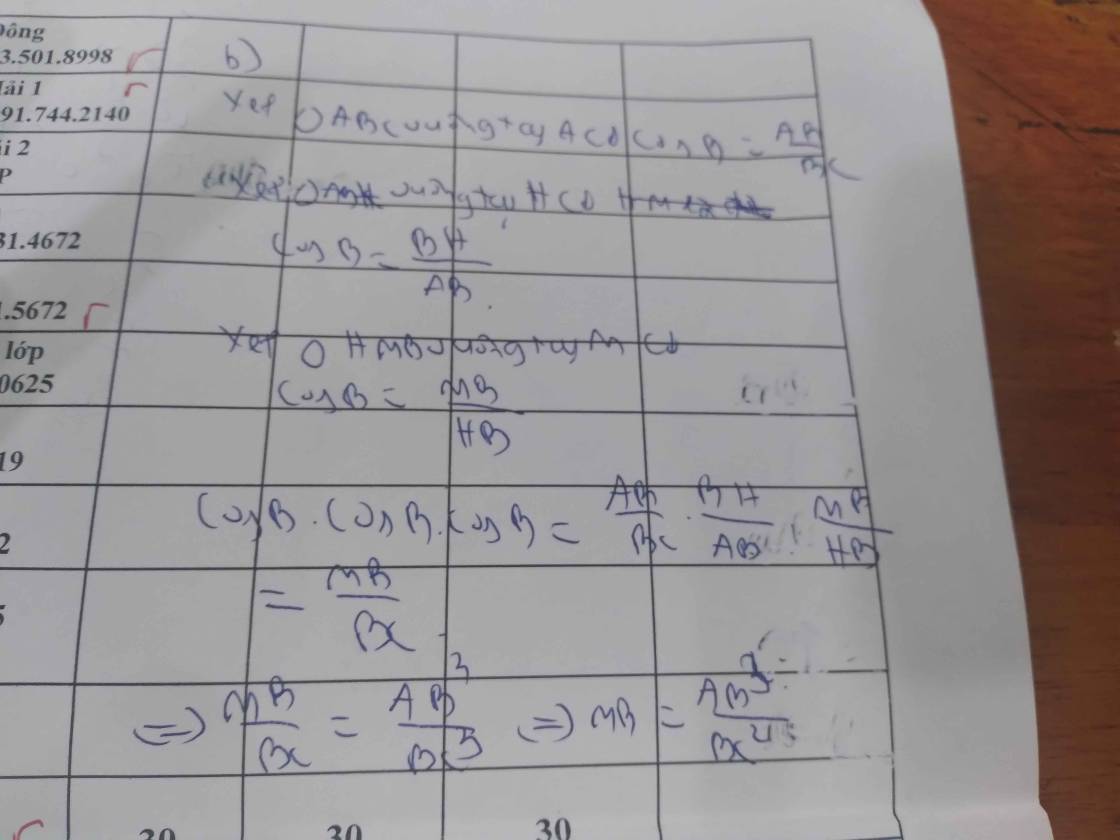
b)Kẻ $H D, H E$ lần lượt vuông góc với $A B, A C$ ( $D$ thuộc $A B, E$ thuộc $A C$ ). Chứng minh $B D \cdot D A+C E \cdot E A=A H^2$.
c)Lấy điểm $M$ nằm giữa $E$ và $C$, kẻ $A I$ vuông góc với $M B$ tại $I$. Chứng minh $\sin \widehat{A M B} \cdot \sin \widehat{A C B}=\dfrac{H I}{C M}$.
1, Xét tg ABC vuông tại H có
BH/AB=sin góc BAC <=> 2000/AB = sin 25° <=> AB=2000/sin 25° sấp sỉ bằng 4732,4(m)
Vậy muốn đạt độ cao 2000m thì mấy bay phải bay đoạn đường 4732,4m
2, ADĐL pytago cho tg ABC vuông tại A có
BC^2=AB^2+AC^2
= 4^2+(4căn 3)^2
=16+48=64
=> BC=8cm
sin góc góc ACB = AB/BC =4/8 =1/2 => góc ACB =30
=> góc ABC =180°- góc BAC - góc ACB
= 180°-90°-30°=60°
b, Xét tam giac AHC vuông tại H,DH là đường cao
Ta có HD^2=BD.DA
Xét tg AHC vuông tại H, đường cao HE có :
HE^2=AE.EC
Vì góc DAgóc AEH=góc EHD=góc HDA =90° nên tứ giác DAEH là hcn.
=> HE= DA
Xét tam giác ADH vuông tại D có
DA^2+DA^2=AH^2
=> HE^2+DH^2 =AH^2(doHE=DA)=>BD.DA+CE.EA=AH^2
Đúng 0
Bình luận (0)
Cho (O) với dây $mathrm{AB}$ cố định (AB không qua $mathrm{O}$ ). Đường kính $mathrm{CD}$ vuông góc với $mathrm{AB}$ tại $mathrm{H}$ (C thuộc cung lớn $mathrm{AB}$ ). Điểm $mathrm{M}$ di chuyển trên cung nhỏ $mathrm{AC}(mathrm{M} neq mathrm{A}$ và $mathrm{M} neq mathrm{C})$. Đường thẳng $mathrm{CM}$ cắt đường thẳng $mathrm{AB}$ tại $mathrm{N}$. Nối $mathrm{MD}$ cắt $mathrm{AB}$ tại $mathrm{E}$.
a) Chứng minh tứ giác CMEH nội tiếp.
b) Chứng minh $mathrm{NM} cdot mathrm{NC}$ NA.NB.
c) Lấy điểm $ma...
Đọc tiếp
Cho (O) với dây $\mathrm{AB}$ cố định (AB không qua $\mathrm{O}$ ). Đường kính $\mathrm{CD}$ vuông góc với $\mathrm{AB}$ tại $\mathrm{H}$ (C thuộc cung lớn $\mathrm{AB}$ ). Điểm $\mathrm{M}$ di chuyển trên cung nhỏ $\mathrm{AC}(\mathrm{M} \neq \mathrm{A}$ và $\mathrm{M} \neq \mathrm{C})$. Đường thẳng $\mathrm{CM}$ cắt đường thẳng $\mathrm{AB}$ tại $\mathrm{N}$. Nối $\mathrm{MD}$ cắt $\mathrm{AB}$ tại $\mathrm{E}$.
a) Chứng minh tứ giác CMEH nội tiếp.
b) Chứng minh $\mathrm{NM} \cdot \mathrm{NC}=$ NA.NB.
c) Lấy điểm $\mathrm{P}$ đối xứng với $\mathrm{A}$ qua $\mathrm{O}$. Gọi I là trung điểm của $\mathrm{MC}$. Kẻ $\mathrm{IK}$ vuông góc với đường thẳng $\mathrm{AM}$ tại $\mathrm{K}$. Chứng minh $\mathrm{IK} / / \mathrm{MP}$ và điểm $\mathrm{K}$ thuộc một đường tròn cố định.
a. Xét (O) , có:
CD \(\perp\)AB = {H}
=> \(\widehat{CHA}=90^o\Rightarrow\widehat{CHE}=90^o\)
Có: \(\widehat{CMD}\)là góc nội tiếp chắn nửa đường tròn đường kính CD
=> \(\widehat{CMD}=90^o\Rightarrow\widehat{CME}=90^o\)
Xét tứ giác CMEH, có:
\(\widehat{CME}+\widehat{CHE}=90^o+90^o=180^o\)
2 góc \(\widehat{CME}\)và \(\widehat{CHE}\)là 2 góc đối nhau
=> CMEH là tứ giác nội tiếp (đpcm)
Câu a: Có góc CHE=90 độ (vì CD\(\perp AB\) tại H)
Góc CMD =90 độ(góc nt chắn nửa đt)
Mà góc CHE và góc CMD ở vị trí đối nhau
⇒ Tứ giác CMEH nội tiếp
Câu b:
Xét \(\Delta NACva\Delta NMB\) có :
Góc N chung
Góc NCA = góc NBM (cùng chắn cung MA)
⇒ \(\Delta NAC\) đồng dạng \(\Delta NBM\) (góc góc)
⇒\(\dfrac{NM}{NA}\)=\(\dfrac{NB}{NC}\)⇔NM.NC=NA.NB
Câu c:
Có góc PMA=90 độ ( góc nt chắn nửa đt)→PM\(\perp\)AK
Mà IK\(\perp\)AK
⇒IK song song với MP (từ vuông góc đến song song
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A đường cao AH AB = 12 cm và BC = 20 cm a tính độ dài AC và đường cao AH b tính tan C và số đo góc C làm tròn đến độ
Cho đường tròn (O,R) .từ điểm A nằm ngoài đường tròn kẻ hai tiếp tuyến AB và AC với đường tròn (B,C là tiếp điểm).AO cắt BC tại H a)cm 4 điểm A,B,O,C cùng thuộc đường tròn b) cm OA vuông góc BC tại H c) cho OA=2R .tính chu vi tam giác ABC theo R d) vẽ cát tuyến AMN với đường tròn.xác định vị trí của cát tuyến AMN sao cho nhỏ nhất .
a: Xét tứ giác ABOC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>ABOC là tứ giác nội tiếp
=>A,B,O,C cùng thuộc một đường tròn
b: Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC và AO là phân giác của góc BAC
Ta có: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
từ (1) và (2) suy ra AO là đường trung trực của BC
=>OA\(\perp\)BC
c: Xét ΔOBA vuông tại B có \(sinBAO=\dfrac{OB}{OA}=\dfrac{1}{2}\)
nên \(\widehat{BAO}=30^0\)
Ta có: AO là phân giác của góc BAC
=>\(\widehat{BAC}=2\cdot\widehat{BAO}=60^0\)
Ta có: ΔOBA vuông tại B
=>\(BO^2+BA^2=OA^2\)
=>\(BA^2=\left(2R\right)^2-R^2=3R^2\)
=>\(BA=R\sqrt{3}\)
Xét ΔBAC có AB=AC và \(\widehat{BAC}=60^0\)
nên ΔBAC đều
=>\(S_{BAC}=\dfrac{BA^2\cdot\sqrt{3}}{4}=\dfrac{3R^2\cdot\sqrt{3}}{4}\)
Đúng 1
Bình luận (0)
Bài 10 (trang 104 SGK Toán 9 Tập 1)
Cho tam giác $ABC$, các đường cao $BD$ và $CE$. Chứng minh rằng :
a) Bốn điểm $B, E, D, C$ cùng thuộc một đường tròn.
b) $DE<BC$.
Lời giải chi tiết
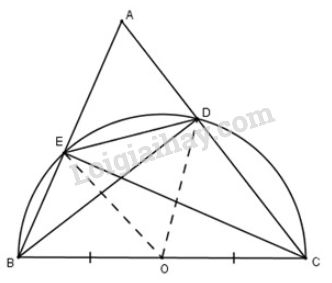
a) Gọi OO là trung điểm của BC⇒OB=OC=BC2.BC⇒OB=OC=BC2. (1)
Vì DODO là đường trung tuyến của tam giác vuông DBCDBC.
Theo tính chất trung tuyến ứng với cạnh huyền, ta có:
OD=12BCOD=12BC (2)
Từ (1) và (2) suy ra OD=OB=OC=12BCOD=OB=OC=12BC
Do đó ba điểm B, D, CB, D, C cùng thuộc đường tròn tâm OO bán kính OBOB.
Lập luận tương tự, tam giác BEC vuông tại E có EO là đường trung tuyến ứng với cạnh huyền BC nên OE=OB=OC=12BCOE=OB=OC=12BC
Suy ra ba điểm B, E, CB, E, C cùng thuộc đường tròn tâm OO bán kính OBOB.
Do đó 4 điểm B, C, D, EB, C, D, E cùng thuộc đường tròn (O)(O) đường kính BCBC.
b) Xét đường (O;BC2)(O;BC2), với BCBC là đường kính.
Ta có DEDE là một dây cung không đi qua tâm nên ta có BC>DEBC>DE ( vì trong một đường tròn, dây lớn nhất là đường kính).
a) Gọi là trung điểm của .
Ta có .
Suy ra
do đó cùng thuộc đường tròn đường kính .
b) Trong đường tròn nói trên, là dây, là đường kính nên
a) Gọi là trung điểm của .
Ta có .
Suy ra
do đó cùng thuộc đường tròn đường kính .
b) Trong đường tròn nói trên, là dây, là đường kính nên
(chú ý : Không xảy ra trường hợp ).
Xem thêm câu trả lời
Bài 2: (2,5 điểm). Cho tam giác ABC vuông tại A, đường cao AH. Biết cạnh AH = 12 , CH = 6cm a) Tính độ dài cạnh BH,AB. b) Gọi M hình chiếu vuông góc kẻ từ H đến AB. Chứng minh: BM = (A * B ^ 3)/(B * C ^ 2) c) Hãy giải tam giác AHC vuông tại H. (Kết quả số đo góc làm tròn đến phút, độ dài làm tròn đến chữ số thập phân thứ hai).
Cho tam giác $A B C$ có trực tâm $\mathrm{H}$, trọng tâm $\mathrm{G}$ và tâm đường tròn ngoại tiếp $\mathrm{O}$. Chứng minh rằng
a) $\overrightarrow{H A}+\overrightarrow{H B}+\overrightarrow{H C}=2 \overrightarrow{H O}$.
b) $\overrightarrow{O A}+\overrightarrow{O B}+\overrightarrow{O C}=\overrightarrow{O H}$.
c) $\overrightarrow{G H}+2 \overrightarrow{G O}=\overrightarrow{0}$.
Giải thích các bước giải:
a) Kẻ đường kính BF.
Ta có: AH⊥BC,CF⊥BC⇒AH//CFAH⊥BC,CF⊥BC⇒AH//CF
Lại có AF⊥AB,CH⊥AB⇒AF//CHAF⊥AB,CH⊥AB⇒AF//CH
⇒AHCF⇒AHCF là hình bình hành.
⇒−−→AH=−−→FC⇒AH→=FC→.
Lại có OIOI là đường trung bình của tam giác BCF nên −→OI=12−−→FCOI→=12FC→
Vậy −−→AH=−−→FC=2−→OIAH→=FC→=2OI→.
b) Ta có: −−→OH=−−→OA+−−→AH=−−→OA+2−→OI=−−→OA+−−→OB+−−→OCOH→=OA→+AH→=OA→+2OI→=OA→+OB→+OC→
c) Do GG là trọng tâm tam giác ABC nên−−→OA+−−→OB+−−→OC=3−−→OG⇒−−→OG=13(−−→OA+−−→OB+−−→OC)=13−−→OHOA→+OB→+OC→=3OG→⇒OG→=13(OA→+OB→+OC→)=13OH→
Vậy ba điểm O,H,GO,H,G thẳng hàng.
Cho tam giác ABC có AB = 6 cm, AC = 4,5 cm và BC = 7,5 cm. a) Chứng minh tam giác ABC vuông tại A. b) Tính các góc B, C và đường cao AH của tam giác đó (Góc làm tròn đến phút, độ dài làm tròn đến chữ số thập phân thứ nhất)
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}=\dfrac{3}{5}\)
nên \(\widehat{B}\simeq36^052'\)
Ta có: ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{C}=90^0-36^052'=53^08'\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(AH\cdot7,5=4,5\cdot6=27\)
=>AH=27/7,5=3,6(cm)
Đúng 1
Bình luận (0)