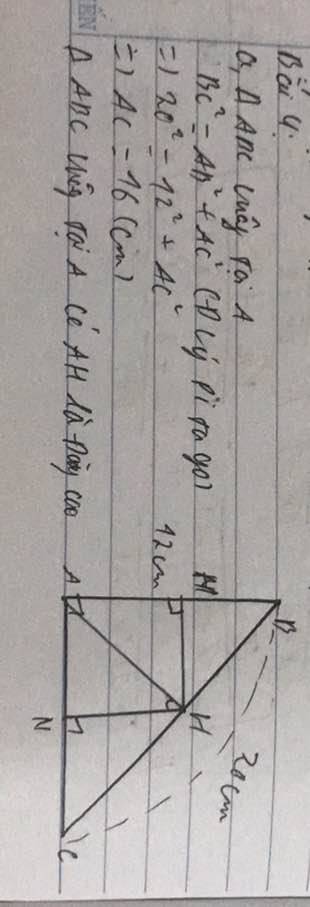
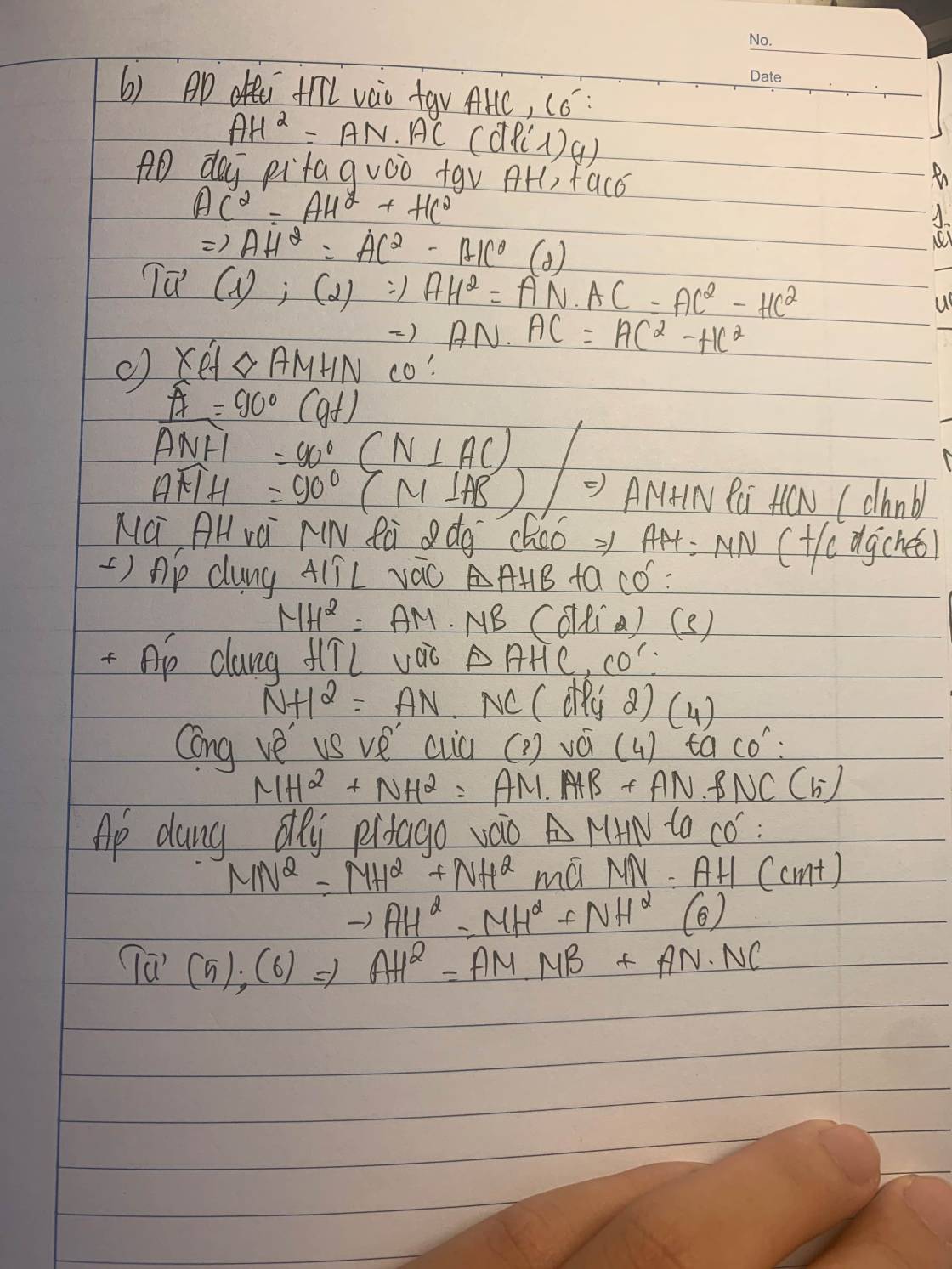(4 điểm) Cho tam giác $A B C$ vuông tại $A$, đường cao $A H(H \in B C)$.
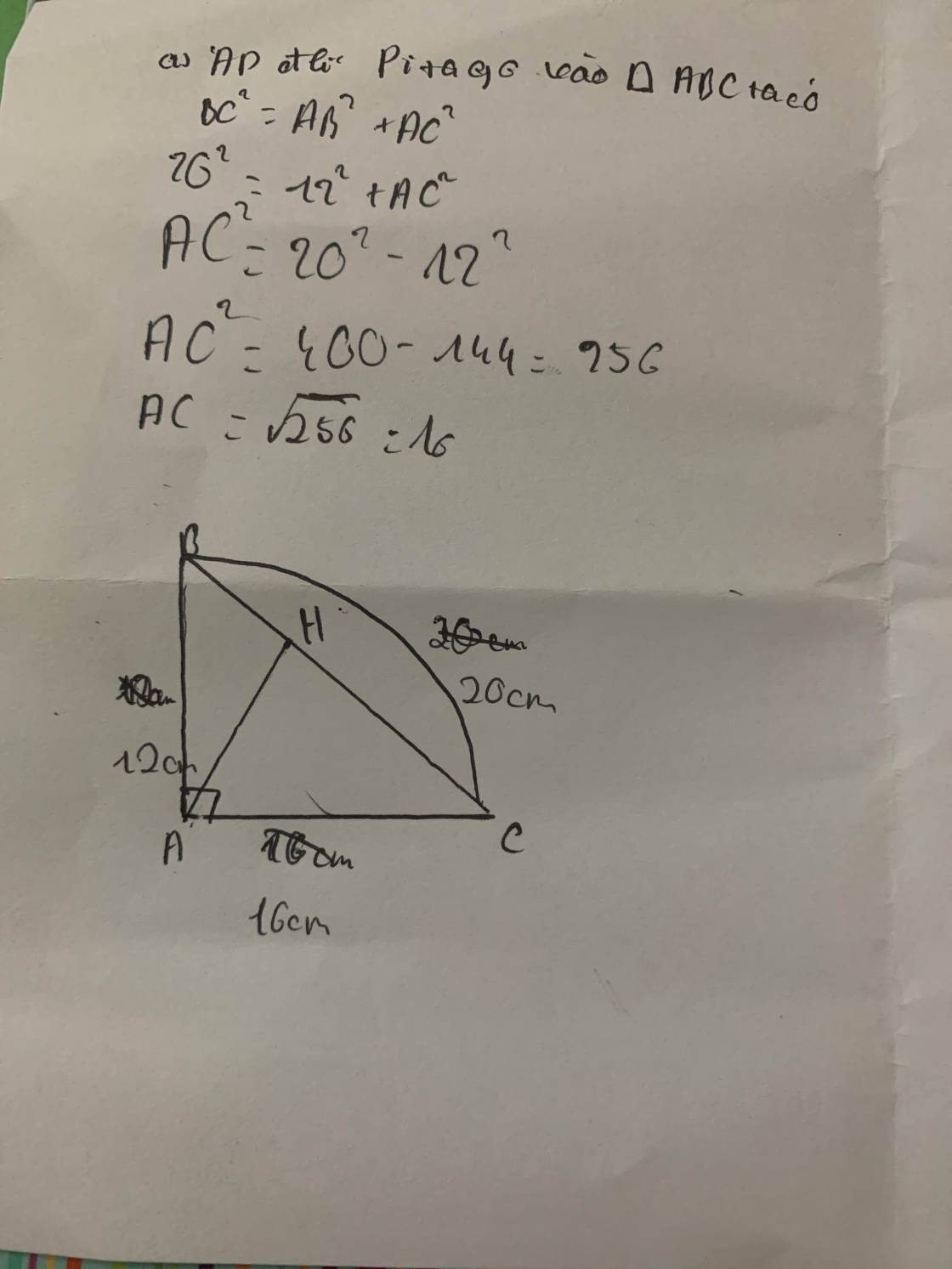
a) Biết $A B=12 \mathrm{~cm}, B C=20 \mathrm{~cm}$, Tính $A C, A H$ và $\widehat{A B C}$ ( làm tròn đến độ);
b) Kẻ $H M$ vuông góc với $A B$ tại $M, H N$ vuông góc với $A C$ tại $N$. Chứng minh: $A N . A C=A C^2-H C^2$
c) Chứng minh: $A H=M N$ và $A M \cdot M B+A N \cdot N C=A H^2$;
d) Chứng minh: $\tan ^3 C=\dfrac{B M}{C N}$.
a/ AC = 16
\(\cos ABC=\dfrac{12}{20}\)
AH = 9,6
b/ Xét tam giác HAC ta có
góc AHC = 90 độ ( AH vuông góc BC giả thiết)
HN vuông góc AN tại N ( gt)
AH2 = AN x AC ( hệ thức lượng trong tam giác vuông) (1)
Mặt khác AH2 = AC2 - HC 2 ( Pitago) (2)
từ (1 ) và (2) ta có AN x AC = AC2 - HC2
a, ADĐL py-ta- go cho tam giác ABC vuông tại A, ta có
BC^2=AB^2+AC^2
20^2=12^2+ AC^2
AC^2 = 20^2 -12^2 =16^2
=> AC=16 cm
Xét tam giác ABC vuông tại A đường cao AH
Ta có: AB.AC= AH.BC ( hệ thức đg cao và các cạnh góc vuông)
=> AH=AB.AC/ BC =12.16/20=9,6
Ta có : sin ABC = AC/BC=16/20=4/5=> góc ABC sấp xỉ bằng 53°
Vậy AC= 16cm,AH =9,6 ; góc ABC sấp xỉ bằng 53°
b, Xét tam giác AHC đg cao HN có
AN.AC= AH^2 (hệ thức giữa đg cao và các cạnh góc vuông) AC^2 =AH^2+HC^2(ĐL pytago)
=> AN.AC= AC^2-HC^2
c, Ta có góc MAN= góc ANH=góc AMH =90°
=> ANHM là hcn => AH=MN
Xét tg AHB ,th AHC và tg MHN có
AM.MB=MH^2
AN.NC= HN^2
MN^2 = HN^2+HM^2
=> AM.MB+AN.NC= HN^2+HM^2=MN^2=AH^2