a,ban nhạc
b,hèn nhát
c,lừa gạt
f,thịt nạc
g,doạ nạt
h,lạc đường
i,dáo dác. Chị chỉ làm thế đc thôi,có đúng ko em?

a ban nhạc

b hẹn nhát

f thịt nạc

g dọa nạt

h lạc đường

xin lỗi có phần chị không dịch được

bản nhạc và lưới mác đúng ko e

Science em nhé!

Khoa học : Science

là science nha 

tíc cho mình đi 

đây nha

Anh chỉ copy trên mạng thôi em nhé , ảnh đây này :

Ừ không sao đâu em 

Chúc em học tốt

Anh nghe nơi chương trình mới của bọn em khó hơn của bọn anh chị nhiều

Học tốt em nhé

Cách làm ngắn gọn: \(5=\dfrac{5\left(x-1\right)}{x-1}=\dfrac{5x-5}{x-1}=\dfrac{5x+5-10}{x-1}\)

Do đó chọn \(f\left(x\right)=5x+5\) thế vào nhanh chóng tính ra kết quả giới hạn

Còn cách khác phức tạp hơn (có thể sử dụng cho tự luận):

Do \(\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-10}{x-1}=5\) hữu hạn nên \(f\left(x\right)-10=0\) có nghiệm \(x=1\)

\(\Rightarrow f\left(1\right)-10=0\Rightarrow f\left(1\right)=10\)

Do đó:

\(\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-10}{\left(\sqrt{x}-1\right)\left(\sqrt{4f\left(x\right)+9}+3\right)}=\lim\limits_{x\rightarrow1}\dfrac{\left[f\left(x\right)-10\right]\left(\sqrt{x}+1\right)}{\left(x-1\right)\left(\sqrt{4f\left(x\right)+9}+3\right)}\)

\(=\lim\limits_{x\rightarrow1}\dfrac{f\left(x\right)-10}{x-1}.\dfrac{\sqrt{x}+1}{\sqrt{4f\left(x\right)+9}+3}=5.\dfrac{1+1}{\sqrt{4f\left(1\right)+9}+3}=5.\dfrac{2}{\sqrt{4.10+9}+3}=...\)

a)\(R_1//R_2\Rightarrow R_{12}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{60\cdot40}{60+40}=24\Omega\)

\(I=\dfrac{U}{R_{tđ}}=\dfrac{12}{24}=0,5A\)

b)\(U_1=U_2=U=12V\)

\(P_1=\dfrac{U_1^2}{R_1}=\dfrac{12^2}{60}=2,4W\)

\(P_2=\dfrac{U_2^2}{R_2}=\dfrac{12^2}{40}=3,6W\)

c)CTM mới: \(R_3nt(R_1//R_2)\)

\(I'=\dfrac{I}{2}=\dfrac{0,5}{2}=0,25A\)

\(R_{tđ}=\dfrac{U}{I'}=\dfrac{12}{0,25}=48\Omega\)

\(R_3=R_{tđ}-R_{12}=48-24=24\Omega\)

Ta có:

+) \(\frac{2013.2012-1}{2013.2012}=1-\frac{1}{2013.2012}\)

+) \(\frac{2012.2011-1}{2012.2011}=1-\frac{1}{2012.2011}\)

Vì \(\frac{1}{2013.2012}< \frac{1}{2012.2011}\Rightarrow1-\frac{1}{2013.2012}>1-\frac{1}{2012.2011}\)

Vậy \(\frac{2013.2012-1}{2013.2012}>\frac{2012.2011-1}{2012.2011}\)

Từ đề bài ta suy ra tất cả các mặt bên của hộp đều là hình thoi (được ghép từ 2 tam giác đều)

\(\Rightarrow A'D=A'B=A'A=a\Rightarrow\) hình chiếu vuông góc của A' lên (ABCD) trùng trọng tâm E của tam giác ABD

\(\widehat{DBE}=\dfrac{1}{2}.60^0=30^0\Rightarrow\widehat{CBE}=\widehat{CBD}+\widehat{DBE}=60^0+30^0=90^0\)

\(\Rightarrow BC\perp BE\)

Mà \(A'E\perp\left(ABCD\right)\Rightarrow A'E\perp BC\)

\(\Rightarrow BC\perp\left(A'BE\right)\Rightarrow BC\perp A'B\)

\(\Rightarrow B'C'\perp A'B\)

\(AE=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\Rightarrow A'E=\sqrt{A'A^2-AE^2}=\dfrac{a\sqrt{6}}{3}\)

Qua C' dựng đường thẳng song song A'E cắt AC tại F \(\Rightarrow C'F=A'E=\dfrac{a\sqrt{6}}{3}\)

\(CF=AE=\dfrac{a\sqrt{3}}{3}\) ; \(AC=2.\dfrac{a\sqrt{3}}{2}=a\sqrt{3}\Rightarrow AF=AC+CF=\dfrac{4a\sqrt{3}}{3}\)

\(\Rightarrow AC'=\sqrt{AF^2+C'F^2}=a\sqrt{6}\)

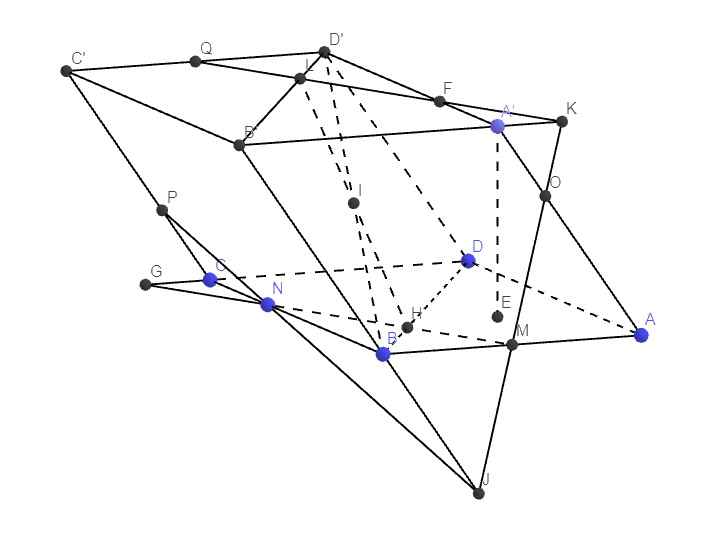
\(CP=\dfrac{1}{3}CC'\) ; \(CN=\dfrac{1}{3}BC\)

Nối PN kéo dài cắt BB' tại J

Talet: \(\dfrac{CP}{BJ}=\dfrac{CN}{NB}=\dfrac{1}{2}\Rightarrow BJ=2CP=\dfrac{2a}{3}\Rightarrow\dfrac{BJ}{B'J}=\dfrac{\dfrac{2a}{3}}{a+\dfrac{2a}{3}}=\dfrac{2}{5}\)

Nối JM cắt A'B' kéo dài tại K

Talet: \(\dfrac{BM}{B'K}=\dfrac{BJ}{B'J}=\dfrac{2}{5}\Rightarrow B'K=\dfrac{5BM}{2}=\dfrac{5a}{4}\)

Nối MN cắt BD tại H và cắt CD tại G

Talet: \(\dfrac{CG}{BM}=\dfrac{CN}{BN}=\dfrac{1}{2}\Rightarrow CG=\dfrac{1}{2}BM=\dfrac{a}{4}\Rightarrow DG=a+\dfrac{a}{4}=\dfrac{5a}{4}\)

Talet: \(\dfrac{BH}{DH}=\dfrac{BM}{DG}=\dfrac{a\div2}{5a\div4}=\dfrac{2}{5}\) (1)

Nối GP cắt C'D' tại Q

Talet: \(\dfrac{CG}{C'Q}=\dfrac{CP}{C'P}=\dfrac{1}{2}\Rightarrow C'Q=2CG=\dfrac{a}{2}\)

Nối QK cắt B'D' tại L

Talet: \(\dfrac{D'L}{B'L}=\dfrac{D'Q}{B'K}=\dfrac{a\div2}{5a\div4}=\dfrac{2}{5}\) (2)

(1);(2) \(\Rightarrow D'L=BH\) (do \(BD=B'D'\))

Nối HL cắt BD' tại I

Talet: \(\dfrac{D'I}{IB}=\dfrac{D'L}{BH}=1\)

Gọi F là giao điểm QK và A'D', O là giao điểm JK và A'A

Ta đồng thời suy ra luôn NPQFOM là thiết diện của (MNP) và chóp