Tìm x sao cho thỏa mãn 45,6<x<47,8

Những câu hỏi liên quan
vẽ đồ thị y=1/2x
tìm A thuộc đồ thị sao cho tọa độ thỏa mãn x+2y=2
tìm B thuộc đồ thị sao cho tọa độ thỏa mãn giá trị tuyệt đối của y-x=2
y=\(\frac{1}{2}\)x =) x=2y
x+2y=2
=) 2y+2y=2
=) y=\(\frac{1}{2}\)
=) x=1
Đúng 0
Bình luận (0)
Tìm m sao cho có x thỏa mãn :
\(\sqrt{x}-1=m-x\)
=>căn x=m-x+1
=>x+căn x-m-1=0(1)
Đặt căn x=a
=>a^2+a-m-1=0(2)
Để (1) có nghiệm thì (2) có nhất 1 nghiệm dương
Δ=1^2-4(-m-1)=1+4m+4=4m+5
TH1: (2) có 2 nghiệm dương
=>4m+5>0 và -1>0 và -m-1>0
=>Loại
TH2: (2) có 1 nghiệm dương, 1 nghiệm âm
=>-m-1<0
=>-m<1
=>m>-1
Đúng 1
Bình luận (0)
1. Cho x,y thỏa mãn: x2 + 5y2 - 4xy + 2y = 3. Tìm x,y sao cho x đạt GTLN
2. Cho x,y thỏa mãn: 3x2 + y2 + 2xy + 4 = 7x + 3y
a) Tìm GTNN, GTLN của biểu thức P = x + y
b) Tìm GTNN, GTLN của x
3. Cho x,y thỏa mãn: x2 + 2y2 + 2xy + 7x + 7y + 10 = 0. Tìm GTLN, GTNN của S = x + y
Tìm số nguyên x thỏa mãn sao cho 5-|x|=1
5-|x|=1
|x|=5-1
|x|=4
=>x = 4 hoac x = -4
Vay x=4 hoac x=-4
Đúng 0
Bình luận (0)
5-|x|=1
5-1=|x|(sử dụng quy tắc chuyển vế)
4=|x|
Vì |4|=|-4|=4
Mà 4 =|x|
=>x=4 hoặc x=-4
Đúng 0
Bình luận (0)
5 - | x | = 1
<=> | x | = 5 - 1
<=> | x | = 4
Mà | 4 | = | - 4 | = 4
=> x = 4 hoặc x = -4
Đúng 0
Bình luận (0)
tìm a,x sao cho : a,x thuộc N*
thỏa mãn x2 + 16 = 25a
Lời giải:
$x^2+16=25^a=(5^a)^2$
$\Rightarrow 16=(5^a)^2-x^2=(5^a-x)(5^a+x)$
$\Rightaarrow 5^a+x\in Ư(16)$
Mà $5^a+x\geq 2$ với mọi $a,x\in\mathbb{N}^*$
$\Rightarrow 5^a+x\in\left\{2; 4;8;16\right\}$
$\Rightarrow 5^a-x\in\left\{8; 4; 2; 1\right\}$
Vì $5^a+x> 5^a-x$ nên $(5^a+x, 5^a-x)\in \left\{(8,2), (16,1)\right\}$
$\Rightarrow (a,x)=(1,3)$
Đúng 0
Bình luận (0)
Tìm số tự nhiên x thỏa mãn sao cho: x+6 =y(x+1)
Tìm số tự nhiên x thỏa mãn sao cho x+6=y(x+1)
x+6=y(x+1)
6=xy+y-x
6=x(y-1)+y
6-1=x(y-1)+(y-1) (trừ cả 2 vế đi 1)
5=(x+1)(y-1)
ta có bảng sau:|
| x+1 | 5 | 1 |
| x | 4 | 0 |
| y-1 | 1 | 5 |
| y | 2 | 6 |
Tìm các số nguyên x,y thỏa mãn:6xy+4x-9y-7=0
Tìm giá trị nhỏ nhất của A=x^3+y^3+xy với x,y dương thỏa mãn x+y=1
Tìm các số nguyên x,y thỏa mãn 2x^2+1/x^2+y^2/4=4 sao cho xy đạt giá trị lớn nhất
HELP !
a) \(6xy+4x-9y-7=0\)
\(\Leftrightarrow2x.\left(3y+2\right)-9y-6-1=0\)
\(\Leftrightarrow2x.\left(3y+x\right)-3.\left(3y+2\right)=1\)
\(\Leftrightarrow\left(2x-3\right).\left(3y+2\right)=1\)
Mà \(x,y\in Z\Rightarrow2x-3;3y+2\in Z\)
Tự làm típ
Đúng 0
Bình luận (0)
\(A=x^3+y^3+xy\)
\(A=\left(x+y\right)\left(x^2-xy+y^2\right)+xy\)
\(A=x^2-xy+y^2+xy\)( vì \(x+y=1\))
\(A=x^2+y^2\)
Áp dụng bất đẳng thức Bunhiakovxky ta có :
\(\left(1^2+1^2\right)\left(x^2+y^2\right)\ge\left(x\cdot1+y\cdot1\right)^2=\left(x+y\right)^2=1\)
\(\Leftrightarrow2\left(x^2+y^2\right)\ge1\)
\(\Leftrightarrow x^2+y^2\ge\frac{1}{2}\)
Hay \(x^3+y^3+xy\ge\frac{1}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=\frac{1}{2}\)
Đúng 0
Bình luận (0)
Tìm các số nguyên thỏa mãn x y sao cho xy+x-y=4
xy+x-y=4
=>(xy+x)-(y+1)=3
=>(y+1)(x-1)=3
Mà x;y nguyên nên (x-1);(y+1) thuộc Ư(3)={1;-1;3;-3}
Đến đây bạn lập bảng là ra
Đúng 0
Bình luận (0)
xy+x-y=4
=>(xy+x)-(y+1)=3
=>(y+1)(x-1)=3
Mà x;y nguyên nên (x-1);(y+1) thuộc Ư(3)={1;-1;3;-3}
Đến đây bạn lập bảng là ra
Đúng 1
Bình luận (0)
\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Tìm số nguyên x, y sao cho số phức z x + yi thỏa mãn z3 18 + 26i A. B. C. D.
Đọc tiếp
Tìm số nguyên x, y sao cho số phức z = x + yi thỏa mãn z3 = 18 + 26i
A. 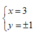
B. 
C. 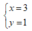
D. 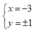
Chọn C.
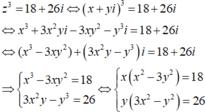
Do x; y nguyên nên
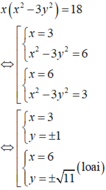
Mà y(3x2 – y2 ) = 26 ⇒ x = 3; y = 1.
Đúng 0
Bình luận (0)


























