Chọn C.
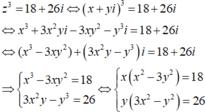
Do x; y nguyên nên
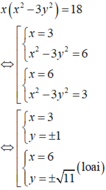
Mà y(3x2 – y2 ) = 26 ⇒ x = 3; y = 1.
Chọn C.
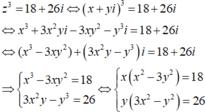
Do x; y nguyên nên
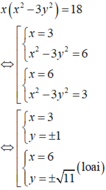
Mà y(3x2 – y2 ) = 26 ⇒ x = 3; y = 1.
Tìm các số nguyên a, b sao cho số phức z = a + b i thỏa mãn z 3 = 2 + 11 i
![]()
![]()
![]()
![]()
Giải phương trình bằng số phức \(x^3=18+26i,z=x+yi\left(x,y\inℤ\right)\)
Cho số phức z = x + y.i thỏa mãn z3 = 2 - 2i. Cặp số là(x;y)
A. (2; 2).
B. (1; 1).
C. (3;-3).
D. (2; -3).
Có bao nhiêu số phức z = x + yi(x,y ∈ ℝ ) thỏa mãn x 2 + y 2 = 5 | x - 2 y | = 4 ?
A. Có 4 số
B. Có 2 số
C. Có 1 số
D. Không có số nào
Tập hợp tất cả các điểm biểu diễn số phức z=x+yi,x,y thuộc R thỏa mãn |z-i|=4 là đường cong có phương trình
A.![]()
B.![]()
C.![]()
D.![]()
Gọi z = x + y i ( x , y ∈ R ) là số phức thỏa mãn hai điều kiện z - 3 2 - 3 2 i và z - 2 2 + z + 2 2 = 26 đạt giá trị lớn nhất. Tính tích x y
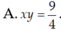
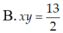
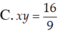
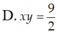
Tìm các số phức z thỏa mãn: z 3 + z ¯ = 0
A. z = 0
B. z = ± 1
C. z = ± i
D. Tất cả đúng.
Trên mặt phẳng phức tập hợp các số phức z = x + yi thỏa mãn |z + 2 - i| = | z ¯ - 3i| là đường thẳng có phương trình
A. y = x + 1
B. y = -x + 1
C. y = -x - 1
D. y = x - 1
Cho số phức z = x + y i với x ; y ∈ R thỏa mãn z - 1 - i ≥ 1 và z - 3 - 3 i ≤ 5 . Gọi m; M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của biểu thức P = x+2y. Tính tỉ số M m
A. 9 4
B. 7 2
C. 5 4
D. 14 5