Theo bà ra ta có : 

\(f\left(2\sqrt{3}\right)=\left(m+1\right)x-2=\left(m+1\right)\left(2\sqrt{3}\right)-2\)

\(=\sqrt{12}\left(m+1\right)-2\)

\(f\left(3\sqrt{2}\right)=\left(m+1\right)x-2=\left(m+1\right)3\sqrt{2}-2\)

\(=\sqrt{18}\left(m+1\right)-2\)

vì 12 < 18 => \(\sqrt{12}< \sqrt{18}\)

hay \(f\left(2\sqrt{3}\right)< f\left(3\sqrt{2}\right)\)

Đáp án D

Đồ thị hàm số y = f ( x ) = x 3 - 3 x + 1  có dạng:

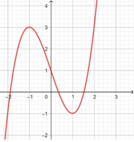
Dựa vào đồ thị ta thấy phương trình f(x) =0 có 3 nghiệm 

\(f'\left(x\right)=4x^3\Rightarrow g\left(x\right)=4x^3-3x^2-6x+1\)

\(g'\left(x\right)=12x^2-6x-6=0\Rightarrow\left[{}\begin{matrix}x_2=-\dfrac{1}{2}\\x_1=1\end{matrix}\right.\)

\(\Rightarrow g\left(-\dfrac{1}{2}\right).g\left(1\right)=\dfrac{11}{4}.\left(-4\right)=-11\)

\(y'=\left(6x^5-6\right)f'\left(x^6-3x^2\right)=0\Rightarrow\left[{}\begin{matrix}x=1\\f'\left(x^6-3x^2\right)=0\end{matrix}\right.\) trong đó \(x=1\) bội lẻ

\(f'\left(x\right)=0\) có các nghiệm \(x=-2;0;2;a;6\)

\(\Rightarrow f'\left(x^6-3x^2\right)=0\Leftrightarrow\) 5 trường hợp:

\(x^6-3x^2=-2\) \(\Leftrightarrow\left(x+1\right)^2\left(x-1\right)^2\left(x^2+2\right)=0\) có 2 nghiệm \(x=-1\) (bội chẵn) và \(x=1\) (bội chẵn)

.... làm tương tự

Riêng với \(x^6-3x^2=a\) thì dựa trên BBT của \(y=x^6-3x^2\) ta thấy pt này có 2 nghiệm đều bội lẻ khi \(4< a< 6\)

Đếm số nghiệm bội lẻ là được