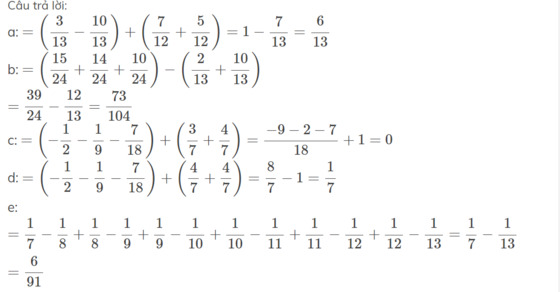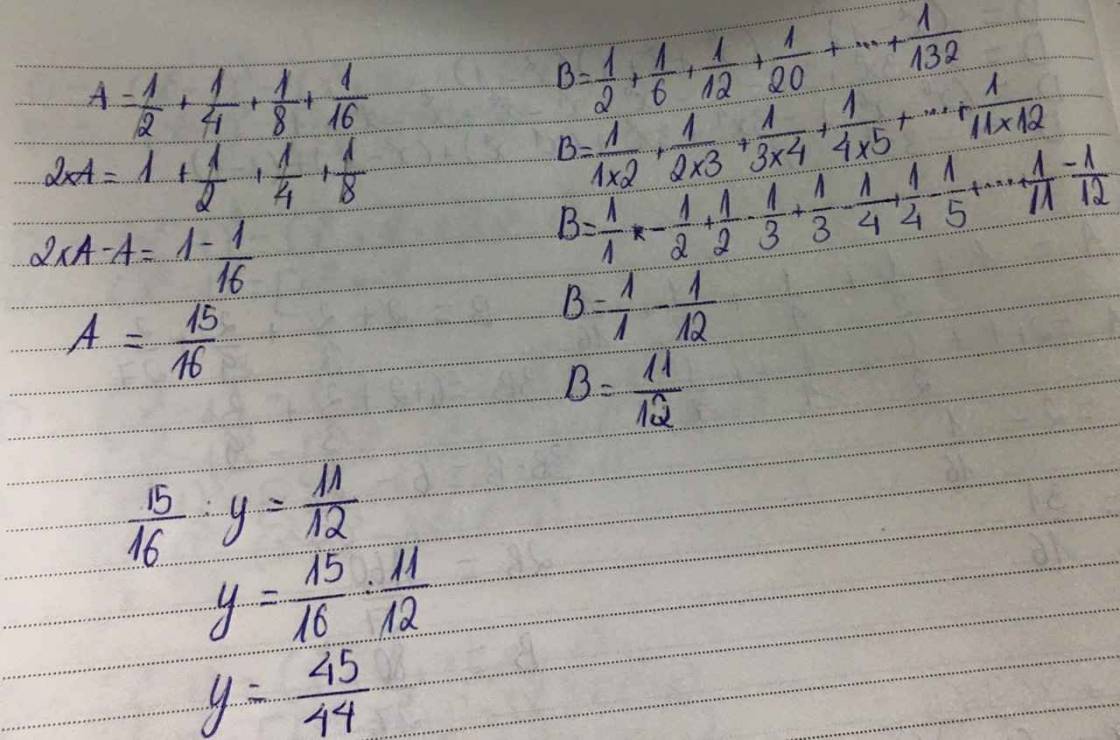A=1/3+1/2+1/6+1/12+1/20+....+1/110+1/132+2/3

Những câu hỏi liên quan
A=1/3+1/2+1/6+1/12+1/20+......+1/110+1/132+2/3
| a) 3/13 + 7/12 - 10/13 + 5/12 | d) -5/10 + 12/28 - 3/27 - 7/18 + 20/35 |
| b) 15/24 - 6/26 + 28/48 - 30/39 + 10/24 | e) 1/56 + 1/72 + 1/90 + 1/110 + 1/132+ 1/156 = |
| c) -1/2 + 3/7 - 1/9 - 7/18 + 4/7 = |
Tính nhanh
1/2+1/6+1/12+1/20+...+1/90+1/110+1/132
\(\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+..........+\frac{1}{132}\)
\(=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+..........+\frac{1}{11.12}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...........+\frac{1}{11}-\frac{1}{12}\)
\(=1-\frac{1}{12}\)
\(=\frac{11}{12}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
1/2+1/6+1/12+1/20+...+1/90+1/110+1/132
mk giải như thề này đ ko ạ
Là sao mik chả hỉu gì cả??????
Ta có : \(\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+...+\frac{1}{90}+\frac{1}{110}+\frac{1}{132}\)
= \(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{9.10}+\frac{1}{10.11}+\frac{1}{11.12}\)
= \(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{9}-\frac{1}{10}+\frac{1}{10}-\frac{1}{11}+\frac{1}{11}-\frac{1}{12}\)
= \(1-\frac{1}{12}=\frac{11}{12}\)
1/2 + 6/ 1 + 12/ 1 + ......... + 1/132 = 1/ 1.2 + 1/2.3 + 1/3.4 + .......... +1/ 11.12 = 1 − 1/2 + 1/'2 − 1/3 + 1/3 − 1/4 + ........... + 1/11 − 1/12 = 1 − 1/12 = 11/12
Tính tổng
\(\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+.........+\frac{1}{110}+\frac{1}{132}\)
=1/1*2+1/2*3+1/3*4+...+1*10*11+1/11*12=1-1/2+1/2-1/3+1/3-1/4+...+1/10-1/11+1/11-1/12
=1-1/12=11/12.
Đúng 0
Bình luận (0)
\(\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+...+\frac{1}{110}+\frac{1}{132}\)
\(=\frac{1}{1\times2}+\frac{1}{2\times3}+\frac{1}{3\times4}+...+\frac{1}{10\times11}+\frac{1}{11\times12}\)
\(=1-\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+....+\frac{1}{11}+\frac{1}{12}\)
\(=1-\frac{1}{12}\)
\(=\frac{11}{12}\)
Đúng 0
Bình luận (0)
\(\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+...+\frac{1}{110}+\frac{1}{132}\)
\(=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{10.11}+\frac{1}{11.12}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{10}-\frac{1}{11}+\frac{1}{11}-\frac{1}{12}\)
\(=1-\frac{1}{12}\)
\(=\frac{11}{12}\)
k mình nha ! Chúc bạn học giỏi ! ^_^
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tính nhanh tổng:1/2+ 1/6+ 1/12+...+1/110+1/132
Bài 3 : Tính nhanh :
a ) A = 2 + 4 + 6 + 8 + ....+ 1000
b ) 1/ 20 + 1/30 + 1/42 + 1/50 + 1/72 + 1/90 + 1/110 + 1/132
c ) 2 / 1x3 + 2 / 3x5 + 2/5 x 7 + .....+ 2 / 97 x 99 + 2/99 x 101
a) A = 2 + 4 + 6 + 8 + ... + 1000
Ta có : A = 2 + 4 + 6 + 8 + ... + 1000 ( có 500 số )
= (1000 + 2) . 500 : 2 = 250500
c) \(\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+...+\frac{2}{97.99}+\frac{2}{99.101}\)
\(=1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{97}-\frac{1}{99}+\frac{1}{99}-\frac{1}{101}\)
\(=1-\frac{1}{101}=\frac{100}{101}\)
Đúng 0
Bình luận (0)
1/2 cộng 1/6 cộng 1/12 cộng .... cộng 1/132
1/90 cộng 1/110 cộng 1/132 cộng ..... cộng 1/10100
1/2 + 1/6 + 1/12 + ... + 1/132
= 1/1.2 + 1/2.3 + 1/3.4 + ... + 1/11.12
= 1/1 - 1/2 + 1/2 - 1/3 + 1/3 - 1/4 + ... + 1/11 - 1/12
= 1 - 1/12
= 11/12
1/90 + 1/110 + 1/132 + ... + 1/10100
= 1/9.10 + 1/10.11 + 1/11.12 + ... + 1/100.101
= ... [như trên]
= 1/9 - 1/100
= 49/450
a) (y+1/3)+(y+2/9)+(y+1/27)+(1/81)=56/81
b) (1/2+1/4+1/8+1/16):y=1/2+1/6+1/12+1/20+...+1/132