Cho a>b>0 và a2 - 6b2 = ab
Tính A = \(\frac{2ab}{a^2-7b^2}\)
Những câu hỏi liên quan
cho a>b>0 và a^2-6b^2=ab. Tính giá trị biểu thức : A=(2ab)/(a^2-7b^2). Tính giá trị biểu thức : A=(2ab)/(a^2-7b^2)
Cho a,b TM a^2-3ab+2b^2+a-b=0 và a^2-2ab+b^2-5a+7b=0 .Chứng minh ab-12a+15b
a) Cho a > b > 0 và a2 - 6b2 =ab Tính giá trị của phân thức \(A=\frac{2ab}{a^2-7b^2}\)
b) Cho a , b , c đôi một khác nhau và a + b + c = 0 chứng mimh rằng \(\frac{9\left(a^2+b^2+c^2\right)}{\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2}=3\)
Vì a + b + c = 0
<=> (a + b + c)2 = 0
<=> a2 + b2 + c2 = -2(ab + bc + ca)
Khi đó \(\frac{9\left(a^2+b^2+c^2\right)}{\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2}=\frac{-18\left(ab+bc+ca\right)}{2\left(a^2+b^2+c^2-ab-bc-ca\right)}\)
\(=\frac{-18\left(ab+bc+ca\right)}{-6\left(ab+bc+ca\right)}=3\)
a2 - 6b2 = ab
<=> (a + 2b)(a - 3b) = 0
<=> \(\orbr{\begin{cases}a=-2b\left(\text{loại}\right)\\a=3b\left(tm\right)\end{cases}}\)
Khi đó \(A=\frac{2ab}{a^2-7b^2}=\frac{6b^2}{2b^2}=3\)
Cho b > 0 ; \(a^2-6b^2\) = ab
Tính giá trị của A = \(\dfrac{2ab}{a^2-7b^2}\)
tìm a,b thuộc Z
a. ab=2a+2b+5
b.ab-7b+5a=0 và b>hoặc=3
c.2ab+3b-4a=1
d.\(\frac{1}{a}+\frac{1}{b}=\frac{1}{2}\)
Tìm các phân thức mới bằng phân thức đã cho và có chung mẫu thức:a)
5
2
x
,
7
x
−
2
y
và
x
−
y
8
y
2
−
2
x...
Đọc tiếp
Tìm các phân thức mới bằng phân thức đã cho và có chung mẫu thức:
a) 5 2 x , 7 x − 2 y và x − y 8 y 2 − 2 x 2 với x ≠ 0 và x ≠ ± 2 y ;
b) 6 b 2 − 5 b + 11 b 3 − 1 , 3 b b 2 + b + 1 và 7 b − 1 với b ≠ 1 .
cho a,b là 2 số thỏa mãn a2+2b2+2ab-4b+4=0.
Tính giá trị biểu thức M=\(\frac{\text{a2-7ab+52}}{a-b}\) với a≠b
\(pt\Leftrightarrow\left(a+b\right)^2+\left(b-2\right)^2=0\)
\(\Leftrightarrow a=-2;b=2\)
Giải tiếp nhé
Đúng 0
Bình luận (1)
Biết các số thực a,b thỏa mãn:
0
b
a
≤
2
và
2
a
b
≤
2
b
+
a
Tìm giá trị lớn nhất của F
a
2
+
b
2
Đọc tiếp
Biết các số thực a,b thỏa mãn: 0 < b < a ≤ 2 và 2 a b ≤ 2 b + a Tìm giá trị lớn nhất của F= a 2 + b 2
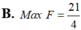
Cho \(a^2-3ab+2b^2+a-b=a^2-2ab+b^2-5a+7b=0\).
C/m \(ab-12a+15b=0\)