Các câu hỏi tương tự
Cho a,b,c là các số thực thỏa mãn
log
2
a
+
b
+
c
a
2
+
b
2
+
c
2
+...
Đọc tiếp
Cho a,b,c là các số thực thỏa mãn log 2 a + b + c a 2 + b 2 + c 2 + 1 = a a - 2 + b b - 2 + c c - 2 Tìm giá trị lớn nhất của biểu thức P = 3 a + 2 b + c a + b + c
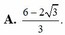
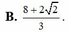
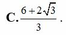
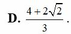
Cho a, b, c, d, e, f là các số thực thỏa mãn
(
d
-
1
)
2
+
e
-
2
2...
Đọc tiếp
Cho a, b, c, d, e, f là các số thực thỏa mãn
( d - 1 ) 2 + e - 2 2 + f - 3 2 = 1 a + 3 2 + b - 2 2 + c 2 = 9
Gọi giá trị lớn nhất, giá trị nhỏ nhất của biểu thức F = a - d 2 + b - e 2 + c - f 2 lần lượt là M, m
Khi đó, M - m bằng:
A. 10
B. 10
C. 8
D. 2 2
Giá trị nhỏ nhất của
P
(
log
a
b
2
)
2
+
6
(
log
b
a
b
a
)
2
với a, b là các số thực tha...
Đọc tiếp
Giá trị nhỏ nhất của P = ( log a b 2 ) 2 + 6 ( log b a b a ) 2 với a, b là các số thực thay đổi thỏa mãn b > a > 1 là:
A. 30.
B. 40.
C. 50.
D. 60.
Cho a , b , c , x , y , z là các số thực thay đổi thỏa mãn
(
x
+
1
)
2
+
(
y
+
1
)
2
+...
Đọc tiếp
Cho a , b , c , x , y , z là các số thực thay đổi thỏa mãn ( x + 1 ) 2 + ( y + 1 ) 2 + ( z - 2 ) 2 = 4 và a + b + c = 6 . Tính giá trị nhỏ nhất của P = ( x - a ) 2 + ( y - b ) 2 + ( z - c ) 2 . .
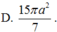
Cho x,y,z,a,b,c là các số thực thay đổi thỏa mãn
(
x
+
3
)
2
+
(
y
-
2
)
2
+
(
z
+
1
)...
Đọc tiếp
Cho x,y,z,a,b,c là các số thực thay đổi thỏa mãn ( x + 3 ) 2 + ( y - 2 ) 2 + ( z + 1 ) 2 = 2 và a+b+c=1. Giá trị nhỏ nhất của biểu thức P = ( x - a ) 2 + ( y - b ) 2 + ( z - c ) 2 là
A. 3 - 2
B. 3 + 2
C. 5 - 2 6
D. 5 + 2 6
Cho các số thực a, b, x 0 và b, x ≠ 1 thỏa mãn
log
x
a
+
2
b
3
log
x
a
+
log
x
b
. Tính giá trị của biểu thức
P
2
a
2
+
3
a
b
+...
Đọc tiếp
Cho các số thực a, b, x > 0 và b, x ≠ 1 thỏa mãn log x a + 2 b 3 = log x a + log x b . Tính giá trị của biểu thức P = 2 a 2 + 3 a b + b 2 a + 2 b - 2 khi a > b
A. 2
B. 2 3
C. 10 27
D. 5 4
Giả sử F(x) là một nguyên hàm của hàm số thỏa mãn F(-2) + F(1) 0 và F(-1) + F(2) 0, với a,b là các số hữu tỷ. Giá trị của 3a+6b bằng A. -4 B. 5 C. 0 D. -3
Đọc tiếp
Giả sử F(x) là một nguyên hàm của hàm số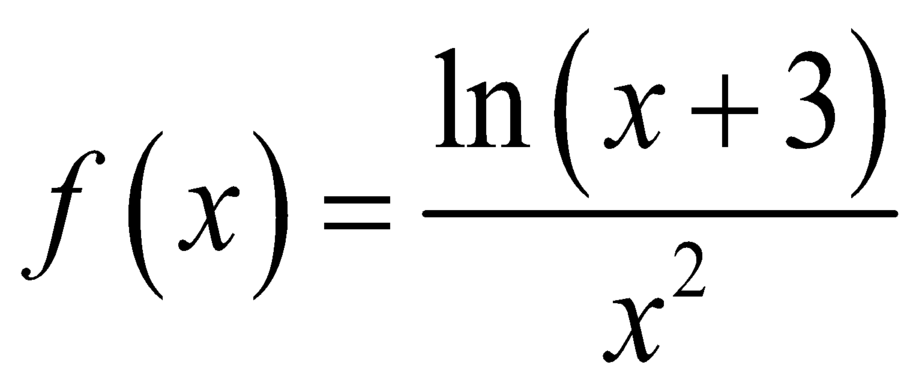 
thỏa mãn F(-2) + F(1) = 0 và F(-1) + F(2) = 0, với a,b là các số hữu tỷ.
Giá trị của 3a+6b bằng
A. -4
B. 5
C. 0
D. -3
cho ba số thực dương a b c thỏa mãn ab+bc+ac≤1. tìm giá trị nhỏ nhất của biểu thức P biết:
P= \(\dfrac{1}{\sqrt{a^2+b^2-abc}}+\dfrac{1}{\sqrt{a^2+c^2-abc}}+\dfrac{1}{\sqrt{c^2+b^2-abc}}\)
Cho số phức
z
a
+
b
i
(
a
,
b
∈
ℝ
;
a
≥
0
;
≥
0
)
. Đặt đa thức
f
(
x
)
a
x
2
+
b
x...
Đọc tiếp
Cho số phức z = a + b i ( a , b ∈ ℝ ; a ≥ 0 ; ≥ 0 ) .
Đặt đa thức f ( x ) = a x 2 + b x - 2 .
Biết f ( - 1 ) ≤ 0 , f ( 1 4 ) ≤ - 5 4 .
Tìm giá trị lớn nhất của z
A. max z = 2 5
B. max z = 3 2
C. max z = 5
D. max z = 2 6