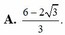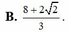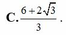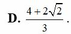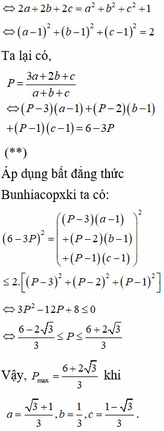Các câu hỏi tương tự
Cho x,y,z,a,b,c là các số thực thay đổi thỏa mãn
(
x
+
3
)
2
+
(
y
-
2
)
2
+
(
z
+
1
)...
Đọc tiếp
Cho x,y,z,a,b,c là các số thực thay đổi thỏa mãn ( x + 3 ) 2 + ( y - 2 ) 2 + ( z + 1 ) 2 = 2 và a+b+c=1. Giá trị nhỏ nhất của biểu thức P = ( x - a ) 2 + ( y - b ) 2 + ( z - c ) 2 là
A. 3 - 2
B. 3 + 2
C. 5 - 2 6
D. 5 + 2 6
cho ba số thực dương a b c thỏa mãn ab+bc+ac≤1. tìm giá trị nhỏ nhất của biểu thức P biết:
P= \(\dfrac{1}{\sqrt{a^2+b^2-abc}}+\dfrac{1}{\sqrt{a^2+c^2-abc}}+\dfrac{1}{\sqrt{c^2+b^2-abc}}\)
Cho a, b, c, d, e, f là các số thực thỏa mãn
(
d
-
1
)
2
+
e
-
2
2...
Đọc tiếp
Cho a, b, c, d, e, f là các số thực thỏa mãn
( d - 1 ) 2 + e - 2 2 + f - 3 2 = 1 a + 3 2 + b - 2 2 + c 2 = 9
Gọi giá trị lớn nhất, giá trị nhỏ nhất của biểu thức F = a - d 2 + b - e 2 + c - f 2 lần lượt là M, m
Khi đó, M - m bằng:
A. 10
B. 10
C. 8
D. 2 2
cho ba số thực dương a b c thỏa mãn ab+bc+ac\(\le\)1. tìm giá trị nhỏ nhất của biểu thức P biết:
P=\(\frac{1}{\sqrt{a^2+b^2-abc}}+\frac{1}{\sqrt{a^2+c^2-abc}}+\frac{1}{\sqrt{c^2+b^2-abc}}\)
Cho a , b , c , x , y , z là các số thực thay đổi thỏa mãn
(
x
+
1
)
2
+
(
y
+
1
)
2
+...
Đọc tiếp
Cho a , b , c , x , y , z là các số thực thay đổi thỏa mãn ( x + 1 ) 2 + ( y + 1 ) 2 + ( z - 2 ) 2 = 4 và a + b + c = 6 . Tính giá trị nhỏ nhất của P = ( x - a ) 2 + ( y - b ) 2 + ( z - c ) 2 . .
![]()
![]()
![]()
Cho a, b, c là các số thực thuộc đoạn [1;2] thỏa mãn
log
2
3
a
+
log
2
3
b
+
log
2
3
c
≤
1
. Khi biểu thức P a3 + b3 + c3 - 3(log2aa + log2bb + log2cc) đạt giá trị lớn nhất thì gi...
Đọc tiếp
Cho a, b, c là các số thực thuộc đoạn [1;2] thỏa mãn log 2 3 a + log 2 3 b + log 2 3 c ≤ 1 . Khi biểu thức P = a3 + b3 + c3 - 3(log2aa + log2bb + log2cc) đạt giá trị lớn nhất thì giá trị của tổng a + b + c là:
A. 2
B. 3 . 2 1 3 3
C. 4
D. 6
Cho ba số thực dương a,b,c thỏa mãn
a
2
+
b
2
+
c
2
-
2
a
+
4
b
-
6
c
10
và a + c2 . Tính giá trị biểu thức P 3a + 2b + c khi
Q
a
2
+
b...
Đọc tiếp
Cho ba số thực dương a,b,c thỏa mãn a 2 + b 2 + c 2 - 2 a + 4 b - 6 c = 10 và a + c=2 . Tính giá trị biểu thức P = 3a + 2b + c khi Q = a 2 + b 2 + c 2 - 14 a - 8 b + 18 c đạt giá trị lớn nhất.
A. 10
B. -10
C. 12
D. -12
Cho a,b,c là các số thực thuộc đoạn [1;2] thỏa mãn
log
2
3
a
+
log
2
3
b
+
log
2
3
c
≤
1
. Khi biểu thức
P
a
3
+
b
3
+
c
3
-
(...
Đọc tiếp
Cho a,b,c là các số thực thuộc đoạn [1;2] thỏa mãn log 2 3 a + log 2 3 b + log 2 3 c ≤ 1 . Khi biểu thức P = a 3 + b 3 + c 3 - ( log 2 a a + log 2 b b + log 2 c c ) đạt giá trị lớn nhất thì giá trị của tổng a + b + c là:
A. 3
B. 3 . 2 1 3 3
C. 4
D. 6
cho hai số a,b là hai số thực đều lớn hơn 1. giá trị nhỏ nhất của biểu thức s=
\(\dfrac{1}{log_{b\sqrt[3]{a}}}\)+\(\dfrac{1}{log\sqrt[3]{ab^2}}\)