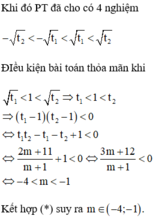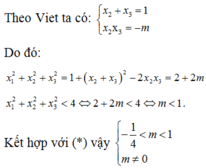tìm m để đths y=x3 + m(x2 -1) cắt trục hoành tại 3 điểm phân biệt

Những câu hỏi liên quan
Tìm m để đồ thị hàm số
y
x
3
-
3
m
x
2
+
3
m
x
-
1
cắt trục Ox tại 3 điểm phân biệt có hoành độ
x
1
;
x
2
;
x
3
thỏa điều kiện
x
1
2
+...
Đọc tiếp
Tìm m để đồ thị hàm số y = x 3 - 3 m x 2 + 3 m x - 1 cắt trục Ox tại 3 điểm phân biệt có hoành độ x 1 ; x 2 ; x 3 thỏa điều kiện x 1 2 + x 2 2 + x 3 2 > 15
A. m ∈ - ∞ ; - 1 3 ∪ 1 ; + ∞
B. m ∈ - ∞ ; - 1 ∪ 1 ; + ∞
C. m ∈ - ∞ ; - 1 ∪ 5 3 ; + ∞
D. m ∈ - ∞ ; - 1 3 ∪ 5 3 ; + ∞
Hoành độ giao điểm của (C) và Ox là nghiệm phương trình
x - 1 x 2 - 3 m - 1 x + 1 = 0 ⇔ x = 1 g x = x 2 - 3 m - 1 x + 1 = 0 1
Để đồ thị hàm số cắt Ox tại 3 điểm phân biệt thì (1) có 2 nghiệm phân biệt khác 1.
Khi đó ∆ > 0 g 1 ≠ 0
⇔ m > 1 m < - 1 3 m ≠ 1 ⇔ m > 1 m < - 1 3
Giả sử x 3 = 1
Theo đề thì phương trình (1) có hai nghiệm x 1 ; x 2
x 1 2 + x 2 2 > 14 ⇔ x 1 + x 2 2 - 2 x 1 x 2 > 14 ⇔ m > 5 3 m < - 1
(thỏa mãn)
Vậy m ∈ - ∞ ; - 1 ∪ 5 3 ; + ∞
Đáp án C
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m để đồ thị hàm số
y
m
+
1
x
4
-
2
2
m
-
3
x
2
+
6
m
+
5
cắt trục hoành tại bốn điểm phân biệt có các hoành độ
x
1...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = m + 1 x 4 - 2 2 m - 3 x 2 + 6 m + 5 cắt trục hoành tại bốn điểm phân biệt có các hoành độ x 1 , x 2 , x 3 , x 4 thỏa mãn x 1 < x 2 < x 3 < 1 < x 4
A. m ∈ - 1 ; - 5 6
B. m ∈ - 3 ; - 1
C. m ∈ - 3 ; 1
D. m ∈ - 4 ; - 1
Để đồ thị hàm số
(
C
)
:
y
x
3
-
2
x
2
+
(
1
-
m
)
x
+
m
(m là tham số) cắt trục hoành tại 3 điểm phân biệt có hoành độ là
x
1
,
x
2
,
x
3...
Đọc tiếp
Để đồ thị hàm số ( C ) : y = x 3 - 2 x 2 + ( 1 - m ) x + m (m là tham số) cắt trục hoành tại 3 điểm phân biệt có hoành độ là x 1 , x 2 , x 3 sao cho x 1 2 + x 2 2 + x 3 2 < 4 thì giá trị của m là:
A. m < 1
B. m > 1 m < - 1 4
C. - 1 4 < m < 1
D. - 1 4 < m < 1 m ≠ 0
Để đồ thị hàm số
(
C
)
:
y
x
3
-
2
x
2
+
(
1
-
m
)
x
+
m
(m là tham số) cắt trục hoành tại 3 điểm phân biệt có hoành độ là
x
1
,
x
2
,
x
3...
Đọc tiếp
Để đồ thị hàm số ( C ) : y = x 3 - 2 x 2 + ( 1 - m ) x + m (m là tham số) cắt trục hoành tại 3 điểm phân biệt có hoành độ là x 1 , x 2 , x 3 sao cho x 1 2 + x 2 2 + x 3 2 < 4 thì giá trị của m là:
![]()

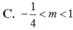
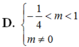
Cho đồ thị
C
m
:
y
x
3
-
2
x
2
+
1
-
m
x
+
m
. Tất cả giá trị của tham số m để
C
m
cắt trục hoành tại ba điểm phân biệt có hoành độ
x...
Đọc tiếp
Cho đồ thị C m : y = x 3 - 2 x 2 + 1 - m x + m . Tất cả giá trị của tham số m để C m cắt trục hoành tại ba điểm phân biệt có hoành độ x 1 , x 2 , x 3 thỏa mãn x 1 2 + x 2 2 + x 3 2 = 4 là
A. m = 1
B. m ≠ 0
C. m = 2
D. m > - 1 4 v à m ≠ 0
Có bao nhiêu giá trị nguyên của tham số m để đồ thị của hàm số
y
x
3
+
(
m
+
2
)
x
2
+
(
m
2
-
m
-
3
)
x
-
m
2
cắt trục hoành tại ba điểm phân biệt A. 3 B. 2 C. 4 D. 1
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để đồ thị của hàm số y = x 3 + ( m + 2 ) x 2 + ( m 2 - m - 3 ) x - m 2 cắt trục hoành tại ba điểm phân biệt
A. 3
B. 2
C. 4
D. 1
Chọn đáp án A
Phương pháp
Nhẩm nghiệm của phương trình hoành độ giao điểm, từ đó tìm điều kiện để phương trình hoành độ giao điểm có 3 nghiệm phân biệt.

Để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt thì phương trình x 2 + ( m + 3 ) x + m 2 = 0 phải có hai nghiệm phân biệt khác 1
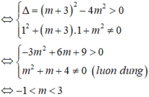
Do đó với -1<m<3 thì đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt
![]()
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m để đồ thị của hàm số y
x
3
+
(
m
+
2
)
x
2
+
(
m
2
m
-
3
)
x
-
m
2
cắt trục hoành tại ba điểm phân biệt? A. 3 B.. 4 C. 1 D. 2
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để đồ thị của hàm số y = x 3 + ( m + 2 ) x 2 + ( m 2 m - 3 ) x - m 2 cắt trục hoành tại ba điểm phân biệt?
A. 3
B.. 4
C. 1
D. 2
Đáp án là A
Phương trình hoành độ giao điểm của đồ thị hàm số đã cho và trục hoành:
![]()
![]()
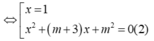
Đồ thị hàm số đã cho cắt trục hoành tại 3 điểm phân biệt ⇔ (1) có 3 nghiệm phân biệt ⇔ (2) có 2 nghiệm phân biệt khác 1
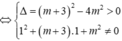
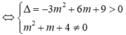
![]()
Do đó có 3 giá trị nguyên của m thỏa mãn ycbt.
Đúng 0
Bình luận (0)
Tìm m để hàm số
y
m
x
3
-
x
2
-
2
x
+
8
m
cắt trục hoành tại 3 điểm phân biệt A.
-
1
6
m
1
2
B.
-
1
6...
Đọc tiếp
Tìm m để hàm số y = m x 3 - x 2 - 2 x + 8 m cắt trục hoành tại 3 điểm phân biệt
A. - 1 6 < m < 1 2
B. - 1 6 < m < 1 2 m ≠ 0
C. - 1 6 ≤ m < 1 2
D. - 1 6 ≤ m < 1 2 m ≠ 0
Phương trình hoành độ giao điểm của đồ thị hàm số đã cho và trục hoành là: m x 3 - x 2 - 2 x + 8 m = 0
⇔ m + 2 m x 2 - 2 m + 1 x + 4 m = 0 ⇔ x = - 2 f x = m x 2 - 2 m + 1 x + 4 m = 0
Yêu cầu bài toán ⇔ phương trình f(x) = 0 có hai nghiệm phân biệt khác -2
⇔ m ≠ 0 ∆ = - 12 m 2 + 4 m + 1 g - 2 = 12 m + 2 ≠ 0 ⇔ - 1 6 < m < 1 2 m ≠ 0
Đáp án B
Đúng 0
Bình luận (0)
Với giá trị nào của tham số m thì (C): yx3-3(m+1) x2+2(m2+4m+1)x-4m(m+1) cắt trục hoành tại ba điểm phân biệt có hoành độ lớn hơn 1? A.
1
2
m
≠
1
B. m 1/ 2 C. m 1/2 D. m
Đọc tiếp
Với giá trị nào của tham số m thì (C): y=x3-3(m+1) x2+2(m2+4m+1)x-4m(m+1) cắt trục hoành tại ba điểm phân biệt có hoành độ lớn hơn 1?
A. 1 2 < m ≠ 1
B. m> 1/ 2
C. m< 1/2
D. m
Phương trình hoành độ giao điểm của đồ thị (C) và trục Ox:
x3-3(m+1) x2+2(m2+4m+1)x-4m(m+1)=0
hay (x-2) (x2-(3m+1) x+2m2+2m)=0

Chọn A.
Đúng 0
Bình luận (0)
Cho hàm số
y
x
3
-
6
x
2
+
9
x
+
m
(m là tham số thực) có đồ thị (C). Gỉa sử (C) cắt trục hoành tại 3 điểm phân biệt có hoành độ
x
1
,
x
2
,
x
3
(với
x
1
x...
Đọc tiếp
Cho hàm số y = x 3 - 6 x 2 + 9 x + m (m là tham số thực) có đồ thị (C). Gỉa sử (C) cắt trục hoành tại 3 điểm phân biệt có hoành độ x 1 , x 2 , x 3 (với x 1 < x 2 < x 3 ). Khẳng định nào sau đây đúng?
A. 0 < x 1 < 1 < x 2 < 3 < x 3 < 4
B . 1 < x 1 < x 2 < 3 < x 3 < 4
C . 1 < x 1 < 3 < x 2 < 4 < x 3
D . x 1 < 0 < 1 < x 2 < 3 < x 3 < 4