Những câu hỏi liên quan
Cho hình chữ nhật ABCD. Gọi H là hình chiếu vuông góc của A trên BD; I và J thứ tự là trung điểm của các đoạn thẳng DH và BC
Tính số đo của góc AIJ
Cho hình chữ nhật ABCD. Gọi H là hình chiếu vuông góc của A trên BD; I và J thứ tự là trung điểm của các đoạn thẳng DH và BC
Tính số đo của góc AIJ
Gọi R là trung điểm AI
Ta có:ID=IH;RA=RH nên IR là đường trung bình tam giác AIH => IR//AD => IR vuông góc với AB
=> R là trực tâm tam giác AIH => BR vuông góc với AI
Do IR là đường trung bình tam giác AIH nên IR//AD//BJ;IR=1/2AD=BJ => BRIJ là hình bình hành => BR//IJ
Mà BR vuông góc với AI nên IJ vuông góc với AI => ^AIJ=900
@Cool Kid : Hình như R là trung điểm của AH mới đúng ?!?!!
Xem thêm câu trả lời
Cho hình bình hành ABCD có AC cắt BD tại O. Gọi H là hình chiếu của A trên DO, K là hình chiếu của O trên AB. Biết góc DAH = HAO = OAB. CMR: DH = OK và ABCD là hình chữ nhật.
Giúp mk vs ạ
Xem chi tiết
Lời giải:
Xét tam giác ADH và AOH có:
\(\widehat{DAH}=\widehat{OAH}\) (gt)
\(\widehat{AHD}=\widehat{AHO}=90^0\)
AH chung
\(\Rightarrow \triangle ADH=\triangle AOH(g.c.g)\) (1)
\(\Rightarrow AD=AO\Rightarrow \frac{AD}{AO}=1\)
Xét tam giác ADH và AOK có:
\(\widehat{AHD}=\widehat{AKO}=90^0\)
\(\widehat{DAH}=\widehat{OAB}=\widehat{OAK}\) (gt)
\(\Rightarrow \triangle ADH\sim \triangle AOK(g.g)\Rightarrow \frac{AH}{AK}=\frac{DH}{OK}=\frac{AD}{AO}=1\Rightarrow AH=AK;DH=OK\)
Vì AO là phân giác của \(\widehat{HAB}\) nên theo tính chất đường phân giác thì:
\(\frac{AH}{AB}=\frac{OH}{OB}\)
Trong đó \(OH=DH\) (do (1)) nên \(OH=\frac{1}{2}OD\). Mà \(OD=OB\) theo tính chất hình bình hành
\(\Rightarrow \frac{AH}{AB}=\frac{OH}{OB}=\frac{1}{2}\)
Mà \(AH=AK\Rightarrow AK=\frac{1}{2}AB\Rightarrow AK=KB\)
Tam giác AOB có OK vừa là đường cao vừa là đường trung tuyến nên tam giác AOB cân tại O. Do đó OA=OB hay AC=BD nên ABCD là hình chữ nhật (đpcm).
Đúng 1
Bình luận (0)
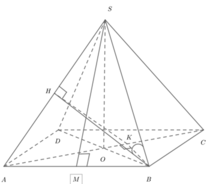
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật với AB a
2
và SASBSCSD2a. Gọi K là hình chiếu vuông góc của B trên AC, H là hình chiếu vuông góc của K trên SA. Tính cosin góc giữa đường thẳng SB và mặt phẳng (BKH).
Đọc tiếp
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật với AB = a 2 và SA=SB=SC=SD=2a. Gọi K là hình chiếu vuông góc của B trên AC, H là hình chiếu vuông góc của K trên SA. Tính cosin góc giữa đường thẳng SB và mặt phẳng (BKH).
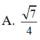
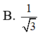
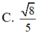
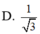
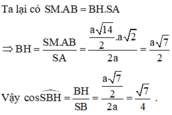
Chọn đáp án A
+ Ta có
![]()
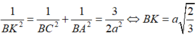
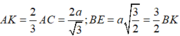
nên K là trọng tâm của tam giác BCD
+ Ta dễ dàng chứng minh được SH ⊥ (BKH) ⇒ SB, (BKH) = SBH
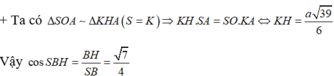
Đúng 1
Bình luận (0)
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật với
A
B
a
2
;
B
C
a
và
S
A
S
B
S
C
S
D
2
a
. Gọi K là hình chiếu vuông góc của B trên AC, H là hình chiếu vuông góc của K trên SA. Tính cosin góc giữa đường thẳng SB...
Đọc tiếp
Cho hình chóp SABCD có đáy ABCD là hình chữ nhật với A B = a 2 ; B C = a và S A = S B = S C = S D = 2 a . Gọi K là hình chiếu vuông góc của B trên AC, H là hình chiếu vuông góc của K trên SA. Tính cosin góc giữa đường thẳng SB và mặt phẳng (BKH).
A. 7 4
B. 1 3
D. 8 5
D. 2 3
Cho hình chữ nhật ABCD ( AB> CB) điểm E đối xứng với B qua A và F đối xứng với B qua C. Kẻ BH vuông góc với EF. Gọi P và Q là hình chiếu của H trên BE và BF. C/m PQ vuông góc với BD
Bài 1: Cho hình thang vuông ABCD có góc A = góc D = 90o , AB = 4cm , CD = 9cm. Tính BD (biết BD vuông góc với BC)
Bài 2: Cho hình thang ABCD , AB//CD , BD là đường cao của hình thang, góc A + góc C = 90o , AB= 1cm, CD= 3cm. Tính AD và BC
Bài 3: Cho hình chữ nhật ABCD, AB= 4cm, AD= 3cm. Gọi E và F là hình chiếu của A và C trên BD. Tính EF
Bài 1: Cho hình thang vuông ABCD có góc A = góc D = 90o , AB = 4cm , CD = 9cm. Tính BD (biết BD vuông góc với BC)
Bài 2: Cho hình thang ABCD , AB//CD , BD là đường cao của hình thang, góc A + góc C = 90o , AB= 1cm, CD= 3cm. Tính AD và BC
Bài 3: Cho hình chữ nhật ABCD, AB= 4cm, AD= 3cm. Gọi E và F là hình chiếu của A và C trên BD. Tính EF
Bài 1: Cho hình thang vuông ABCD có góc A = góc D = 90o , AB = 4cm , CD = 9cm. Tính BD (biết BD vuông góc với BC)
Bài 2: Cho hình thang ABCD , AB//CD , BD là đường cao của hình thang, góc A + góc C = 90o , AB= 1cm, CD= 3cm. Tính AD và BC
Bài 3: Cho hình chữ nhật ABCD, AB= 4cm, AD= 3cm. Gọi E và F là hình chiếu của A và C trên BD. Tính EF
Cho hình chữ nhật ABCD có AB=2AD. Gọi H là hình chiếu của A trên BD. Trên đoạn BH lấy điểm M sao cho HM=HA. Qua M kẻ đường thẳng vuông góc với BH cắt BA ở N. Chứng minh M là trung điểm của BH.
Cíu!!! Quên hết kiến thức r.