Gọi I là giao điểm của EG và AC. Chứng minh, D,B,I thẳng hàng
Gợi ý: Kẻ AK // DG
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, đường phân giác BD. Kẻ DK _|_ BC. Gọi I là giao điểm của AK và BD.
a) Chứng minh: BD _|_ AK.
b) Kẻ AH _|_ BC. CMR: AK là tia phân giác của góc HAC.
c) Kẻ Cx // AK. Cx cắt AK tại M. CMR: 3 điểm B, A, M thẳng hàng.
d) Chứng minh AC + KM > AK + MC.
Cho tam giác ABC vuông tại A. Tia phân giác góc B cắt cạnh AC tại điểm M. Kẻ
M
D
⊥
B
C
(
D
∈
B
C
)
.
a) Chứng minh BA BD.b) Gọi E là giao điểm của hai đường thẳng DM và BA. Chứng minh
∆
A
B
C
∆
D
B
E
.
c) Kẻ
D
H
⊥
M
C
(
H
∈
M
C...
Đọc tiếp
Cho tam giác ABC vuông tại A. Tia phân giác góc B cắt cạnh AC tại điểm M. Kẻ M D ⊥ B C ( D ∈ B C ) .
a) Chứng minh BA = BD.
b) Gọi E là giao điểm của hai đường thẳng DM và BA. Chứng minh ∆ A B C = ∆ D B E .
c) Kẻ D H ⊥ M C ( H ∈ M C ) và A K ⊥ M E ( K ∈ M E ) . Gọi N là giao điểm của hai tia DH và AK. Chứng minh MN là tia phân giác góc HMK.
d) Chứng minh ba điểm B, M, N thẳng hàng.
Cho tam giác ABC vuông tại A (AB AC) có đường cao AH. Kẻ HD vuông góc với AB (D thuộc AB), kẻ HE vuông góc với AC (E thuộc AC) a) Chứng minh tứ giác ADHE là hình chữ nhật. b) Gọi I là trung điểm của đoạn thẳng HC. Gọi K là điểm đối xứng với điểm A qua điểm I. Chứng minh rằng AC // HK. c) Chứng minh tứ giác DECK là hình thang cân. d) Gọi O là giao điểm của DE và AH; Gọi M là giao điểm của AI và CO. Chứng minh AM 1/3 AK
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC) có đường cao AH. Kẻ HD vuông góc với AB (D thuộc AB), kẻ HE vuông góc với AC (E thuộc AC) a) Chứng minh tứ giác ADHE là hình chữ nhật. b) Gọi I là trung điểm của đoạn thẳng HC. Gọi K là điểm đối xứng với điểm A qua điểm I. Chứng minh rằng AC // HK. c) Chứng minh tứ giác DECK là hình thang cân. d) Gọi O là giao điểm của DE và AH; Gọi M là giao điểm của AI và CO. Chứng minh AM = 1/3 AK
Bài 6: Cho tam giác ABC vuông tại A (AB<AC), đường cao AH. Từ H kẻ HE và HF lần lượt
vuông góc với AB và AC (EAB, FAC).
a. Chứng minh AH=EF.
b. Trên tia FC xác định điểm G sao cho FG=AF. Chứng minh tứ giác EFGH là hình
bình hành.
c. Gọi O là giao điểm của AH và EF, I là giao điểm của EG và FH, kẻ trung tuyến FK
của tam giác HFC. Chứng minh ba điểm O; I; K thẳng hàng.
Cho hai hình vuông ABCD và BEFG sao cho A,B,E thẳng hàng theo thứ tự đó và BEBA. Gọi H là giao điểm của EG và DF.a) Cm: HDHF.b) Gọi I là giao điểm của CF và AE. Cm: D,G,I thẳng hàng.c) Trên AB lấy điểm K sao cho AKBG. Cm: tam giác KFC và tam giác DFE có cùng trọng tâm.d) Cm: DE,AF,CB đồng quy tại I; CF,DG,AB đồng quy tại K.e) Gọi M,N lần lượt là tâm của hình vuông ABCD và hình vuông BEFG. Cm: M,I,N,K thẳng hàng.
Đọc tiếp
Cho hai hình vuông ABCD và BEFG sao cho A,B,E thẳng hàng theo thứ tự đó và BE<BA. Gọi H là giao điểm của EG và DF.
a) Cm: HD=HF.
b) Gọi I là giao điểm của CF và AE. Cm: D,G,I thẳng hàng.
c) Trên AB lấy điểm K sao cho AK=BG. Cm: tam giác KFC và tam giác DFE có cùng trọng tâm.
d) Cm: DE,AF,CB đồng quy tại I; CF,DG,AB đồng quy tại K.
e) Gọi M,N lần lượt là tâm của hình vuông ABCD và hình vuông BEFG. Cm: M,I,N,K thẳng hàng.
Cho hai hình vuông ABCD và BEFG sao cho A,B,E thẳng hàng theo thứ tự đó và BEBA. Gọi H là giao điểm của EG và DF.a) Cm: HDHF.b) Gọi I là giao điểm của CF và AE. Cm: D,G,I thẳng hàng.c) Trên AB lấy điểm K sao cho AKBG. Cm: tam giác KFC và tam giác DFE có cùng trọng tâm.d) Cm: DE,AF,CB đồng quy tại I; CF,DG,AB đồng quy tại K.e) Gọi M,N lần lượt là tâm của hình vuông ABCD và hình vuông BEFG. Cm: M,I,N,K thẳng hàng.
Đọc tiếp
Cho hai hình vuông ABCD và BEFG sao cho A,B,E thẳng hàng theo thứ tự đó và BE<BA. Gọi H là giao điểm của EG và DF.
a) Cm: HD=HF.
b) Gọi I là giao điểm của CF và AE. Cm: D,G,I thẳng hàng.
c) Trên AB lấy điểm K sao cho AK=BG. Cm: tam giác KFC và tam giác DFE có cùng trọng tâm.
d) Cm: DE,AF,CB đồng quy tại I; CF,DG,AB đồng quy tại K.
e) Gọi M,N lần lượt là tâm của hình vuông ABCD và hình vuông BEFG. Cm: M,I,N,K thẳng hàng.
Cho tam giác ABC vuông tại A. Tia phân giác góc B cắt cạnh AC tại điểm M. Kẻ MD⊥BC (D thuộc BC)
a) Chứng minh BA = BD.
b) Gọi E là giao điểm của hai đường thẳng DM và BA. Chứng minh △ABC = △DBE
c) Kẻ DH ⊥ MC ( H∈MC) và AK ⊥ ME ( K∈ME). Gọi N là giao điểm của DH và AK. Chứng minh MN là tia phân giác của góc HMK.
d) Chứng minh ba điểm B, M, N thẳng hàng.
nếu bạn ko thấy ảnh thì zô thống kê hỏi đáp của mình là thấy bài này nhá . ( cậu tìm câu nào có câu này r ấn zô xem nha )
hoặc link bài của mình nè
https://scontent-hkt1-1.xx.fbcdn.net/v/t1.15752-9/89947717_345887062999332_7304147707155709952_n.jpg?_nc_cat=110&_nc_sid=b96e70&_nc_ohc=Hj57duZ44dcAX91P2ra&_nc_ht=scontent-hkt1-1.xx&oh=7ea184f17776bd230198145c38f92aae&oe=5E95F1D5
Dễ vãi nồi
Cho ABC cân ở A. Có góc A nhọn Gọi I là trung điểm của BC . Kẻ BD vuông góc với AC tại D , kẻ CE vuông góc với AB tại E . Gọi K là giao điểm của BD và CE .
Chứng minh rằng: a) Δ BCE= ΔCBD
b) Δ BEK= ΔCDK và AK là tia phân giác của góc BAC
c) Ba điểm A,K,I thẳng hàng
Cho tam giác ABC vuông tại A, đường phân giác BD (D∈AC). Từ D kẻ DH vuông góc với BC.a) Chứng minh ΔABD ΔHBD.b) So sánh AD và DC.c) Gọi K là giao điểm của đường thẳng AB và DH, I là trung điểm của KC. Chứng minh 3 điểm B, D, I thẳng hàng
Đọc tiếp
Cho tam giác ABC vuông tại A, đường phân giác BD (D∈AC). Từ D kẻ DH vuông góc với BC.
a) Chứng minh ΔABD = ΔHBD.
b) So sánh AD và DC.
c) Gọi K là giao điểm của đường thẳng AB và DH, I là trung điểm của KC. Chứng minh 3 điểm B, D, I thẳng hàng
a: Xét ΔBAD vuông tại A và ΔBHD vuông tại H co
BD chung
góc ABD=góc HBD
=>ΔBAD=ΔBHD
b: DA=DH
DH<DC
=>DA<DC
c: Xét ΔBHK vuông tại H và ΔBAC vuông tại A có
BH=BA
góc HBK chung
=>ΔBHK=ΔBAC
=>BK=BC
=>ΔBKC can tại B
mà BI là trung tuyến
nên BI là phân giác của góc KBC
mà BD là phân giác
nên B,D,I thẳng hàng
Đúng 3
Bình luận (2)
Cho tam giác ABC vuông tại A, đường phân giác BD (D∈AC). Từ D kẻ DH vuông góc với BC.
a) Chứng minh ΔABD = ΔHBD.
b) So sánh AD và DC.
c) Gọi K là giao điểm của đường thẳng AB và DH, I là trung điểm của KC. Chứng minh 3 điểm B, D, I thẳng hàng.
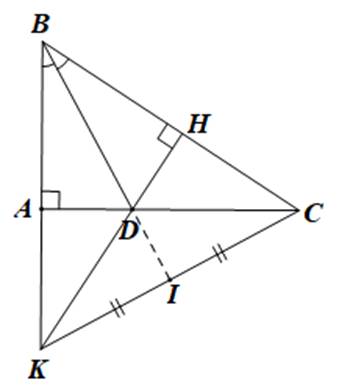
a) Xét \(\Delta\)\(\text{ }\text{ABD}\) và \(\text{ΔHBD}\) có
\(\widehat{\text{BAD}}=\widehat{\text{BHD}}=\text{90}^{\text{o}}\)
\(\text{BD}\) là cạnh chung
\(\widehat{\text{ABD}}=\widehat{\text{HBD}}\) (do \(\text{BD}\) là tia phân giác của \(\widehat{\text{ABD}}\) )
Vậy \(\text{ΔABD = ΔHBD}\) (cạnh huyền – góc nhọn)
___________________________________________________
b) Từ \(\text{ΔABD = ΔHBD}\) (câu a) suy ra\(\text{ AD = HD}\) (hai cạnh tương ứng)
Xét \(\text{ΔDHC}\) vuông tại \(\text{H}\) có \(\text{DC}\) là cạnh huyền nên \(\text{DC}\) là cạnh lớn nhất
Do đó \(\text{DC}\)\(>\text{HD}\) nên \(\text{DC}>AD\)
________________________________________________________
c) Xét \(\text{ΔBKC}\) có \(\text{CA ⊥ BK, KH ⊥ BC}\) và \(\text{CA}\) cắt \(\text{KH}\) tại \(\text{D}\)
Do đó \(\text{D}\) là trực tâm của \(\text{BKC}\), nên \(\text{BD ⊥ KC (1)}\)
Gọi \(\text{J}\) là giao điểm của \(\text{BD và KC}\)
Xét \(\text{ΔBKJ}\) và \(\text{ΔBCJ}\) có
\(\widehat{\text{BJK}}=\widehat{BJC}=90^o\)
\(\text{BJ}\) là cạnh chung
\(\widehat{\text{KBJ}}=\widehat{\text{CBJ}}\) (do \(\text{BJ}\) là tia phân giác của \(\widehat{\text{ABD}}\) )
\(\Rightarrow\) \(\text{ΔBKJ = ΔBCJ}\) (cạnh góc vuông – góc nhọn kề)
Suy ra\(\text{ KJ = CJ}\) (hai cạnh tương ứng)
Hay \(\text{J}\) là trung điểm của \(\text{KC}\)
theo bài ra : \(\text{I}\) là trung điểm của \(\text{KC}\) nên \(\text{I}\) và \(\text{J}\) trùng nhau.
Vậy \(\text{B, D, I}\) thẳng hàng
Đúng 2
Bình luận (0)
