Ôn tập cuối năm môn Hình học
Các câu hỏi tương tự
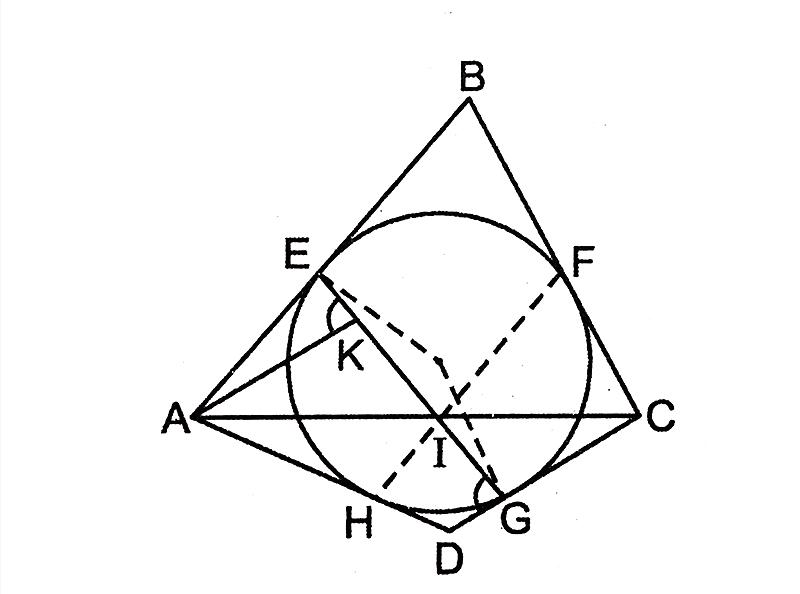
Bài 1: Cho ∆ABC đều, kẻ AH vuông góc với BC tại H. Trên tia đối của tia BC lấy điểm E sao cho BE BC. Trên tia đối của tia CB lấy điểm D sao cho CB CD. a) Chứng minh rằng ∆AEB ∆ADC b) Từ D kẻ DF vuông góc với AC tại F. Chứng minh rằng ∆CHF cân c) Chứng minh rằng AD//HF d) Từ B kẻ BM vuông góc AE tại M, từ C kẻ CN vuông góc với AD tại N. Gọi I là giao điểm của BM và CN. Chứng minh AI là phân giác của 𝐵𝐴𝐶
Bài 2: Cho ∆ABC có AB AC 5cm, BC 6CM. Kẻ AK vuông góc với BC ( K ∈ BC). a) Chứng minh rằ...
Đọc tiếp
Bài 1: Cho ∆ABC đều, kẻ AH vuông góc với BC tại H. Trên tia đối của tia BC lấy điểm E sao cho BE = BC. Trên tia đối của tia CB lấy điểm D sao cho CB = CD. a) Chứng minh rằng ∆AEB = ∆ADC b) Từ D kẻ DF vuông góc với AC tại F. Chứng minh rằng ∆CHF cân c) Chứng minh rằng AD//HF d) Từ B kẻ BM vuông góc AE tại M, từ C kẻ CN vuông góc với AD tại N. Gọi I là giao điểm của BM và CN. Chứng minh AI là phân giác của 𝐵𝐴𝐶
Bài 2: Cho ∆ABC có AB= AC = 5cm, BC = 6CM. Kẻ AK vuông góc với BC ( K ∈ BC). a) Chứng minh rằng KB = KC và 𝐵𝐴𝐾 ̂ =𝐶𝐴𝐾 ̂ b) Tính độ dài AK c) Kẻ KE vuông góc với AB ( E ∈ AB) , KD vuông góc với AC ( D ∈ AC). Chứng minh rằng ∆KDE là tam giác cân. d) Chứng minh rằng DE//BC e) Trên tia đối của tia AB lấy điểm M sao cho AB = AM. Chứng minh răng MC vuông góc với BC
Bài 3: Cho ∆ABC vuông tại B. Trên tia đối của tia BC lấy điểm D sao cho BD = BC a) Chứng minh rằng 𝐵𝐴𝐶 ̂ = 𝐵𝐴𝐷 ̂ b) Tính độ dài CD biết AB = 4cm, AC = 5 cm c) Kẻ BE vuông góc với AC ( E ∈ AC); BH vuông góc với AD ( H ∈ AD). ∆HBE là tam giác gì? Tại sao? d) ∆ABC cần có thêm điều kiện gì để ∆HBE đều
Cho tam giác ABC cân tại A(AB>BC).Gọi I là trung điểm AB.Qua I kẻ đừờng thẳng vuông góc với AB và cắt đừờng thẳng BC tại D.
A)Chứng minh tam giác DIB=tam giác DIA.
B)Trên tia đối của AD lấy E sao cho AE=CD.Chứng minh BE=DA.
C)Chứng minh BE>DI
cho tam giác ABC vuông ở Acos AH là đường cao,AM là trung tuyến .gọi D là điểm đối xứng với M qua D
a, chứng minh M và E đối xứng với nhau qua AB
b, chứng minh AMBE là hình thoi
c, kẻ HK vuông góc với AB,HI vuông góc với AC chứng minh IK vuông góc với AM
d, gọi S là điểm đối xứng với H qua K chứng minh B,S E thẳng hàng
Cho tam giác cân DEF (DE=DF) .Gọi M,N lần lượt là trung điểm của DF và DE.
a) chướng minh EM=FN và góc DEM = góc DFN
b)Gọi K là giao điểm của EM và FN .chứng minh KE=KF
C) chứng minh DK là tia phân giác của góc EDF
d) DK kéo dài cắt EK tại H . Chứng minh H là trung điểm của EF
e) chứng minh DH vuông góc EF
Cho tam giác nhọn ABC . M thuộc BC ,gọi D là điểm đx với M qua AB, E đx với M qua AC . Gọi I,K là giao điểm của DE với AB,AC.
cmr MA là tia phân giác của góc IMK . b,tìm vị trí của điểm M để DE có độ dài nhỏ nhất
cho tam giác ABC có góc A vuông , D và E lần lượt là trung điểm của AB,BC.trên tia ED lấy F sao cho D là trung điểm EF , gọi CF giao với AE tại G , DG giao với AC tại I.CM:EC^2+2AC^2=EF^2
Cho tam giác ABC có góc A90 độ và đường phân giác BH (H thuộc AC).Kẻ HM vuông góc với BC (M thuộc BC).Gọi N là giao của AB và MH .Chứng minh
a, Tam giác ABHMBH
b,BH là trung trực của AM
c,AM//CN
d,BH vuông góc CN
e,Tam giác BNC cân
f, Gọi BH cắt NC tại M. Chúng minh M là trung điểm NC
g, HCHM
GIÚP TUI VỚI MAI THI CUỐI KÌ 2 RÙI!!!TUI CẢM ƠN TRƯỚC NHỮNG NGƯỜI ĐÃ GIÚP TUI(quan trọng là phần e,f,g thôu còn a,b,c,d tui biết làm rùi)
Đọc tiếp
Cho tam giác ABC có góc A=90 độ và đường phân giác BH (H thuộc AC).Kẻ HM vuông góc với BC (M thuộc BC).Gọi N là giao của AB và MH .Chứng minh
a, Tam giác ABH=MBH
b,BH là trung trực của AM
c,AM//CN
d,BH vuông góc CN
e,Tam giác BNC cân
f, Gọi BH cắt NC tại M. Chúng minh M là trung điểm NC
g, HC>HM
GIÚP TUI VỚI MAI THI CUỐI KÌ 2 RÙI!!!TUI CẢM ƠN TRƯỚC NHỮNG NGƯỜI ĐÃ GIÚP TUI(quan trọng là phần e,f,g thôu còn a,b,c,d tui biết làm rùi)
Cho hình vuông ABCD, M là trung điểm của CD. Gọi K là điểm nằm trên đường thẳng BD sao cho K không trùng với D và AK vuông góc với KM. Tính tỉ số DK/DB.☕
Từ điêm A nằm ngoài đường tròn (O) tã vẽ tiếp tuyến AB và cắt tuyến ACD với đường tròn sao cho tia AO nằm giữa AB và AD (B:tiếp điểm;C nằm giữa A và D).Gọi M là trung điểm của CD. a) cm AB^2=AC×AD b) cm tứ giác ABOM nt đường tròn (I) . ĐỊNH TÂM I c) đường tròn I cắt đường tròn O tại E. Cm AE là tiếp tuyến của đường tròn
cho tam giác ABC (AB<AC) trên cạnh AB và AC lấy điểm D và E sao cho BD=CE Gọi I là trung điểm của DE vẽ P sao cho I là trung điểm của BP 1)chứng minh hai tam IDP VÀ IEP bằng nhau từ đó suy ra AB//EP 2,CMR:BAC=2ECP 3,lây M là điểm bất kì trên AC xác định vị trí của M để MB+MP nhỏ nhất