Giúp em giải bài này với:
Cho A=40+41+42+...+42016 và B=42017 : 3Tính B - A
A, Chứng tỏ rằng: M = 75.(42017+ 42016 +42 +4 + 1) +25 chia hết cho 10² 6+.
các bạn giải giúp mình bài này với:cho a là số gồm 2n chữ số 1,b là số gồm n+1 chữ số 1,c là số gồm n chữ số 6.CMR a+b+c+8 là số chính phương
Ai giải được bài này thì cố gắng giúp mình nha ^^
a=1.....1(2n số 1)=1....1(n số 1).\(10^n\) +1...1(n số 1)
b=1...1(n+1 số 1)=1...1(n số 1).10+1
c=6...6(n số 6)=6.1...1(n số1)
Đặt m=1...1(n số 1) \(\Rightarrow10^n\) =9m+1
a+b+c+8=m.(9m+2)+10m+1+6m+8=9m^2+18m+9=(3m+3)^2 là số chính phương
Bài Toàn 16 : Tính tổng
a) S = 1 + 2 + 22 + 23 + … + 22017
b) S = 3 + 32 + 33 + ….+ 32017
c) S = 4 + 42 + 43 + … + 42017
d) S = 5 + 52 + 53 + … + 52017
a.
$S=1+2+2^2+2^3+...+2^{2017}$
$2S=2+2^2+2^3+2^4+...+2^{2018}$
$\Rightarrow 2S-S=(2+2^2+2^3+2^4+...+2^{2018}) - (1+2+2^2+2^3+...+2^{2017})$
$\Rightarrow S=2^{2018}-1$
b.
$S=3+3^2+3^3+...+3^{2017}$
$3S=3^2+3^3+3^4+...+3^{2018}$
$\Rightarrow 3S-S=(3^2+3^3+3^4+...+3^{2018})-(3+3^2+3^3+...+3^{2017})$
$\Rightarrow 2S=3^{2018}-3$
$\Rightarrow S=\frac{3^{2018}-3}{2}$
Câu c, d bạn làm tương tự a,b.
c. Nhân S với 4. Kết quả: $S=\frac{4^{2018}-4}{3}$
d. Nhân S với 5. Kết quả: $S=\frac{5^{2018}-5}{4}$
Cho mình hỏi nốt bài này thôi :3
Tính giá trị biểu thức:
a) M = x2 (x + y) - x2y - x3 tại x = - 2017 và y = 2017
b) N = a3 - 3a2 - a(3 - a)
Giúp mình nốt bài này thôi pls
b: \(N=a^3-3a^2-a\left(3-a\right)\)
\(=a^2\left(a-3\right)+a\left(a-3\right)\)
\(=a\left(a-3\right)\left(a+1\right)\)
a) M = x2 (x + y) - x2y - x3 tại x = - 2017 và y = 2017
M= \(x^3+x^2y-x^2y-x^3\)
M = 0
b) N = a3 - 3a2 - a(3 - a)
N = \(a^3-3a^2-3a+a^2\)
N =\(a^3-2a^2-3a\)
cho A= 21/40 + 23/27 + 19/44 và B= 13/38 + 23/30 + 18/41
Không tính giá trị cụ thể của A và B, hãy so sánh A và B.
Hãy giải bài toán trên và cho biết đã sử dụng những cách so sánh phân số nào?
( mọi người giúp em với, em cảm ơn mọi người)
21/40>13/38 vì cả tử số và mẫu số của phân số 21/40 lớn hơn tử số và mẫu số của phân số 13/38.
23/27>23/30 vì có mẫu số bé hơn nên phân số đó lớn hơn.
19/44>18/41 vì cả tử số và mẫu số của phân số 19/44 lớn hơn tử số và mẫu số của phân số 18/41.
vậy A>B.
a)Cho a.b = 7 và a + b = - 6 Tính a^3 + b^3
a)Cho a.b = 40 và a - b = 3Tính a^3 - b^3
a) Ta có: \(a^3+b^3\)
\(=\left(a+b\right)^3-3ab\left(a+b\right)\)
Thay \(ab=40\) và \(a+b=-6\) vào biểu thức ta có
\(\left(-6\right)^3-3\cdot7\cdot\left(-6\right)=-90\)
b) Ta có: \(a^3-b^3\)
\(=\left(a-b\right)^3+3ab\left(a-b\right)\)
Thay \(ab=40\) và \(a-b=3\) vào biểu thức ta có:
\(3^3+3\cdot40\cdot3=387\)
a: a^3+b^3=(a+b)^3-3ab(a+b)
=(-6)^3-3*7*(-6)
=-90
b: a^3-b^3=(a-b)^3+3ab(a-b)
=3^3+3*40*3
=387
Cho bài toán sau đây:
40-41+42-43+44-45+46-47+48-49+50-51+52-53+54-55+56-57+58
Các bạn hãy giải câu hỏi này giúp mình nhé! Thanks!!!
Đú đởn ăn chơi học hành sa sút đến nỗi có bài toán đơn giản như zậy mà cũng phải hỏi !
40-41+42-43+44-45+46-47+48-49+50-51+52-53+54-55+56-57+58=
=40+(42-41)+(44-43)+(46-45)+(48-47)+(50-49)+(52-51)+(54-53)+(56-55)+(58-57)=49
chơi ff ko xin id
giúp mình giải bài sau với:
Cho hai đường thẳng y = 2x + 2 (d₁) và y = 6 - 2x (d2)
a/ Vẽ (d₁) và (d2) trên cùng một mặt phẳng tọa độ.
b/ Tìm tọa độ giao điểm của (d₁) và (d2) bằng phép tính.
c/ Tìm a,b của đường thẳng (d) y=ax+b biết đường thẳng (d) cắt đường thẳng y = x - 6 tại một điểm trên trục tung và cắt đường cắt đường thẳng y = 2x+1 tại điểm có hoành độ bằng 2.
a: 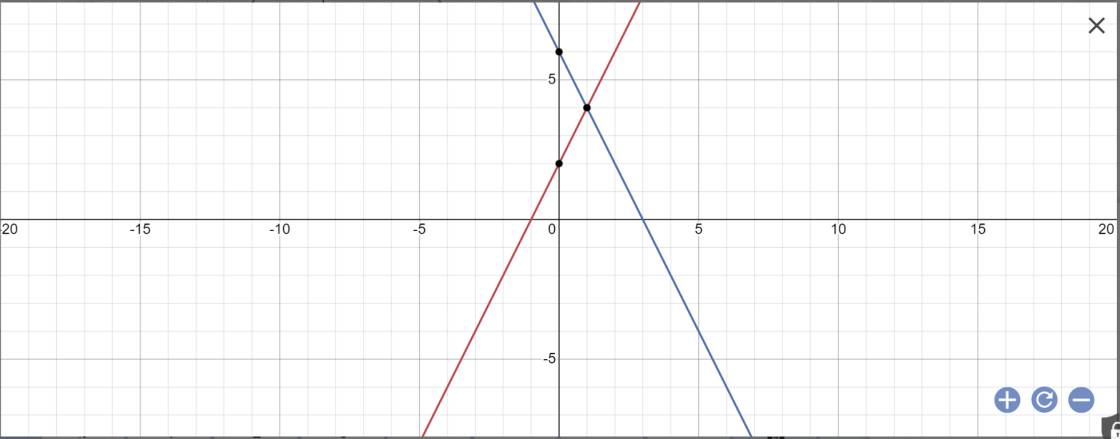
b: Phương trình hoành độ giao điểm là:
2x+2=6-2x
=>2x+2x=6-2
=>4x=4
=>x=1
Thay x=1 vào y=2x+2, ta được:
\(y=2\cdot1+2=4\)
Vậy: (d1) cắt (d2) tại A(1;4)
c: Thay x=0 vào y=x-6, ta được:
y=0-6=-6
Thay x=0 và y=-6 vào y=ax+b, ta được:
\(a\cdot0+b=-6\)
=>b=-6
=>y=ax-6
Thay x=2 vào y=2x+1, ta được:
\(y=2\cdot2+1=5\)
Thay x=2 và y=5 vào y=ax-6, ta được:
2a-6=5
=>2a=11
=>\(a=\dfrac{11}{2}\)
Ai giải bài này hộ mình với:cho A=1/3+1/6+1/10+1/15+...+1/55+1/66.Hãy so sánh A với 1
do những số đó bé hơn 1 nên cộng lại vẫn bé hơn 1
A = \(\dfrac{1}{3}\) + \(\dfrac{1}{6}\) + \(\dfrac{1}{10}\) + \(\dfrac{1}{15}\) + ..+ \(\dfrac{1}{55}\)+ \(\dfrac{1}{66}\)
A = 2 \(\times\) ( \(\dfrac{1}{6}\) + \(\dfrac{1}{12}\) + \(\dfrac{1}{20}\) + \(\dfrac{1}{30}\) +...+ \(\dfrac{1}{110}\) + \(\dfrac{1}{132}\))
A = 2 \(\times\) ( \(\dfrac{1}{2.3}\) + \(\dfrac{1}{3.4}\) + \(\dfrac{1}{4.5}\)+ \(\dfrac{1}{5.6}\) +...+ \(\dfrac{1}{10.11}\)+ \(\dfrac{1}{11.12}\))
A = 2 \(\times\) ( \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\) + \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\) + \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) + \(\dfrac{1}{5}\) - \(\dfrac{1}{6}\) +...+ \(\dfrac{1}{10}\) - \(\dfrac{1}{11}\)+ \(\dfrac{1}{11}\) - \(\dfrac{1}{12}\))
A = 2 \(\times\) ( \(\dfrac{1}{2}\) - \(\dfrac{1}{12}\))
A = 1 - \(\dfrac{1}{6}\) < 1
Vậy A = \(\dfrac{1}{3}\) + \(\dfrac{1}{6}\) + \(\dfrac{1}{10}\) + \(\dfrac{1}{15}\) + ...+ \(\dfrac{1}{55}\)+ \(\dfrac{1}{66}\) < 1
Ai giải giúp mình bài này với:cho đoạn thẳng AB và điểm M nằm giữa A,B. Vẽ các tam giác đều MAC và MBD trên cùng nửa mặt phẳng bờ AB. Các tia AC và BD cắt nhau tại O. Gọi I,K lần lượt là cá trung điểm của AD và BC. Chứng minh:
a) tam giác AOB đều
b) MC = OD và MD =OC
c) AD = BC
d) tam giác MIK đều
Mình cảm ơn nhiều
a) ta có tam giác MAC đều suy ra CAM= 60 độ
tam giác DBM đều suy ra DBM= 60 độ
suy ra tam giác AOB cân suy ra OA=OB
mà A=60 độ
suy ra tam giác AOB đều( trong 1 tam giác cân nếu có 1 góc bằng 60 độ thì đó là tam giác đều)
Nếu M là trung điểm AB:
a)
Tam giác CAM cân nên CA=AM=MC;\(\widehat{CAM}\)= \(\widehat{CMA}\)= \(\widehat{MCA}\)=60 độ
Tam giác DMB cân nên DM=MB=BD;\(\widehat{DMB}\)= \(\widehat{MBD}\)= \(\widehat{MDB}\)=60 độ
Mà AM=MB \(\Rightarrow\)CA=AM=MC=DM=MB=BD
\(\widehat{AMC}\)+\(\widehat{CMD}\)+\(\widehat{DMB}\)=180 độ
Mà \(\widehat{AMC}\)=\(\widehat{BMD}\)=60 độ \(\Rightarrow\)\(\widehat{CMD}\)=60 độ
Tam giác CMD có MC=MD;\(\widehat{CMD}\)=60 độ nên tam giác CMD là tam giác đều\(\Rightarrow\)\(\widehat{MDC}\)=\(\widehat{MCD}\)=60 độ
Ta có \(\widehat{ACM}\)+\(\widehat{MCD}\)+\(\widehat{DCO}\)=180 độ mà \(\widehat{ACM}\)=\(\widehat{MCD}\)= 60 độ \(\Rightarrow\)\(\widehat{DCO}\)=60 độ
Tương tự \(\widehat{CDO}\)=60 độ
\(\Rightarrow\)\(\widehat{COD}\)=60 độ
Tam giác OCD có ba góc bằng 60 độ nên tam giác đó là tam giác đều nên CD=DO=OC
\(\Rightarrow\)CD=DO=OC=CA=AM=MC=MB=DB=DM
\(\Rightarrow\)AB=AO=OB\(\Rightarrow\)tam giác AOB đều
b)Từ câu a) ta có MC=OD;MD=OC
c)
Xét tam giác ACB và tam giác BDA
có AB chung; AC=DB;\(\widehat{CAB}\)=\(\widehat{DBA}\)=60 độ \(\Rightarrow\)tam giác ACB = tam giác BDA\(\Rightarrow\)AD = CB
Nếu M không trung điểm AB thì mình không biết làm.