Tìm khoảng cách từ điểm 6 đến điểm -2 trên trục số.

Những câu hỏi liên quan
Quan sát trục số:
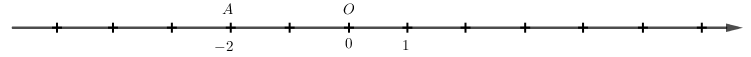
a) Tính khoảng cách từ điểm O đến điểm A.
b) Tìm trên trục số những điểm cách điểm O một khoảng là 5 đơn vị.
a) Khoảng cách từ điểm O đến điểm A: 2 đơn vị.
b) Những điểm cách O một khoảng là 5 đơn vị là: điểm 5 và -5.
Đúng 5
Bình luận (0)
a) Khoảng cách từ điểm O đến điểm A = |0-(-2)| = 2
b) Các điểm cách O một khoảng 5 đơn vị là: -7 và 3
Đúng 0
Bình luận (1)
a) Khoảng cách từ điểm O đến điểm A: 2 đơn vị.
b) Những điểm cách O một khoảng là 5 đơn vị là: điểm 5 và -5.
Đúng 0
Bình luận (0)
Trên mặt phẳng tọa độ Oxy, vẽ đồ thị (d) của hàm số y=-x+2
Tìm tọa độ của những điểm nàm trên đường thẳng (d) sao cho khoảng cách từ điểm đó đến trục Ox bằng hai lần khoảng cách từ điểm đó đến trục Oy
Bài 1: Cho hàm số y=f(x)=ax4-bx2+x+3. Biết f(2)=17. Tính f(-2)
Bài 2: Cho(d):y=-x+2
a) Vẽ (d)
b) Tìm các điểm nằm trên (d) sao cho khoảng cách từ điểm đó đến trục Ox bằng 2 làn khoảng cách từ đó đến trục Oy
Trên 2 trục số, so sánh khoảng cách từ điểm 0 đến hai điểm \(\sqrt 2 \) và \( - \sqrt 2 \).

Ta thấy khoảng cách từ 0 đến điểm \(\sqrt 2 \) bằng \(\sqrt 2 \).
Khoảng cách từ 0 đến điểm -\(\sqrt 2 \) bằng \(\sqrt 2 \)
Vậy khoảng cách từ 0 đến hai điểm \(\sqrt 2 \) và \( - \sqrt 2 \) bằng nhau.
Đúng 0
Bình luận (0)
Khoảng cách từ điểm 0 đến điểm √22 là √22.
Khoảng cách từ điểm 0 đến điểm -√22 là √22.
Do đó khoảng cách từ điểm 0 đến điểm √22 và khoảng cách từ điểm 0 đến điểm −√2-2 là bằng nhau vì đều bằng √22.
Đúng 0
Bình luận (0)
a) Hãy biểu diễn hai số -5 và 5 trên cùng một trục số.
b) Tính khoảng cách từ điểm 5 đến điểm 0.
c) Tính khoảng cách từ điểm -5 đến điểm 0.
a)

b) Khoảng cách từ điểm 5 đến điểm 0 là: 5 đơn vị
c) Khoảng cách từ điểm - 5 đến điểm 0 là: 5 đơn vị
Đúng 0
Bình luận (0)
khoảng cách từ điểm a đến điểm -1 trên trục số là 7. tìm giá trị của a biết a>0
Ta có a là: (-1) + 7 = 6
| 6 | = 6
vậy giá trị tuyệt đối của a là 6
Đúng 0
Bình luận (0)
tìm trên (d): y=2x+3 các điểm có khoảng cách đến trục tung= 2 lần khoảng cách đến trục hoành
Mn giúp vs ak
khoảng cách đến từ -7 đến điểm 0 trên trục số
Khoảng cách từ -7 đến điểm 0 trên trục số : 7
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm toạ độ của điểm M thuộc parabol y = ax2, biết rằng parabol đi qua điểm A(-2 ; -2) và khoảng cách từ M đến trục hoành gấp đôi khoảng cách từ M đến trục tung.
Gọi parabol có dạng y=ax2
Vì P đi qua A(-2;-2)\(\Rightarrow\)a=-\(\dfrac{1}{2}\)
\(\Rightarrow\)P có dạng y= -\(\dfrac{1}{2}\)x2 (1)
vì khoảng cách đến trục hoành gấp đôi khoảng cách đến trục tung\(\Rightarrow\)\(\left|y\right|\)=2\(\left|x\right|\)
Nếu x>0 thì y>0 (vô lí)
Nếu x<0 thì y<0\(\Rightarrow\)y=-2x (2)
Từ (1) và (2) có x=4 và y=-2
hoặc x=-4 và y= -2
vậy M(4;-2) hoặc(-4;-2)
Xem thêm câu trả lời






















