Cho đoạn thẳng AB vẽ về 2 phía của DC các đoạn thẳng AC và BD vuông góc với AB sao cho AC=BA. Chứng Minh góc ADC = góc BCD

Những câu hỏi liên quan
Cho đoạn thẳng AB. Vẽ về hai phía của AB các đoạn thẳng AC và BD vuông góc với AB sao cho AC=BD. Chứng minh rằng góc ADC=góc BCD
Vi \(AB⊥AC\)
\(AB⊥BC\)
=> AC // BC
Mặt khác AC = BD
=> AC // BD (theo tính chất đoạn chắn - đảo)
=> \(\widehat{ADC}=\widehat{BCD}\)
Đúng 0
Bình luận (0)
Vì AB vuông góc với AC
AB vuông góc với BC
Suy ra AC song song với BC
Mà AC = BD
Suy ra góc ACD = góc BCD
Đúng 0
Bình luận (0)
ta có: AC//BD ( CÙNG VUÔNG GÓC VỚI AB)
mà: AC=BD
suy ra t/g ACBD là hình bình hành
suy ra: AD//BC
suy ra: đpcm
Cho △ABC AB<AC . kẻ AH vuông góc với BC. vẽ đoạn thẳng BD = BA, BD vuông góc với BA sao cho C và D khác phía với AB. Vẽ đoạn thẳng CE = CA, CE vuông góc với CA sao cho B và E khác phía với AC. Kẻ DI vuông góc với Bc, EK vuông góc với BC. Chứng minh :
a) IH =DI + AH
b) BI + CK
Em ơi em nhập lại câu hỏi nha!
Đúng 1
Bình luận (0)
a) IH DI + AHb) BI + CK
Đọc tiếp
a) IH =DI + AH
b) BI + CK
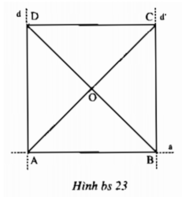
Vẽ đường thẳng a. Trên đường thẳng a vẽ đoạn thẳng AB 4 (cm). Vẽ đường thẳng d đi qua điểm A và vuông góc với a. Vẽ đường thẳng d’ đi qua điểm B và vuông góc với a. Trên đường thẳng d lấy điểm D sao cho AD AB. Trên đường thẳng d’ lấy điểm C sao cho hai điểm C, D nằm về cùng phía với đường thẳng a và BC AB. Vẽ các đoạn thẳng CD, AC, BD. Gọi O là giao điểm của AC và BD.a) Đo và cho biết số đo góc ADC.b) Đo và cho biết số đo góc BCD.C) Đo và cho biết số đo góc BOC
Đọc tiếp
Vẽ đường thẳng a. Trên đường thẳng a vẽ đoạn thẳng AB = 4 (cm). Vẽ đường thẳng d đi qua điểm A và vuông góc với a. Vẽ đường thẳng d’ đi qua điểm B và vuông góc với a. Trên đường thẳng d lấy điểm D sao cho AD = AB. Trên đường thẳng d’ lấy điểm C sao cho hai điểm C, D nằm về cùng phía với đường thẳng a và BC = AB. Vẽ các đoạn thẳng CD, AC, BD. Gọi O là giao điểm của AC và BD.
a) Đo và cho biết số đo góc ADC.
b) Đo và cho biết số đo góc BCD.
C) Đo và cho biết số đo góc BOC
Ở cùng phía của đoạn thẳng AB , vẽ góc BAx = góc ABy = 120 độ. Trên tia Ax và By lần lượt lấy C và D sao cho AC = BD . Chứng minh 1) BC = AD 2) Góc BCD = góc ADC help me !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! cả hình nữa nha
Xem chi tiết
1: Xét ΔBAC và ΔABD có
AB chung
góc BAC=góc ABD
AC=BD
Do đó: ΔBAC=ΔABD
=>BC=AD
2: ΔBAC=ΔABD
=>góc ABC=góc BAD
góc ABC+góc DBC=góc ABD
góc BAD+góc CAD=góc CAB
mà góc ABD=góc CAB và góc ABC=góc BAD
nên góc DBC=góc CAD
Xét ΔCAD và ΔDBC có
CA=DB
góc CAD=góc DBC
AD=BC
Do đó: ΔCAD=ΔDBC
=>góc BCD=góc ADC
Đúng 0
Bình luận (0)
Cho tam giác ABC có ba góc nhọn. Vẽ đoạn thẳng AD vuông góc với AB và bằng AB (D khác phía C đối với AB), vẽ đoạn thẳng AE vuông góc với AC và bằng AC (E khác phía B đối với AC).Chứng minh rằng: DC = BE
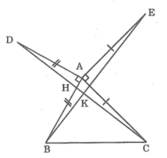
∠DAC = ∠DAB + ∠BAC = 90o + ∠BAC
∠BAE = ∠BAC + ∠CAE = ∠BAC + 90o
⇒ ∠DAC = ∠BAE
Xét ΔABE và ΔADC, ta có:

Đúng 1
Bình luận (0)
Cho tam giác ABC có ba góc nhọn. Vẽ đoạn thẳng AD vuông góc với AB và bằng AB (D khác phía C đối với AB), vẽ đoạn thẳng AE vuông góc với AC và bằng AC (E khác phía B đối với AC).Chứng minh rằng: DC ⊥BE
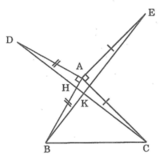
Gọi giao điểm DC và AB là H, giao điểm của CD và BE là K
Ta có: ΔABE = ΔADC (cmt)
⇒ ∠ABE = ∠ADC (hai góc t.ư)
hay ∠HBK = ∠ADH
+ ΔADH và ΔBKH đều có tổng ba góc trong mỗi tam giác bằng 180o nên có:
∠ADH + ∠DAH + ∠AHD = ∠BKH + ∠KHB + ∠HBK
Mà ∠AHD = ∠BHK (hai góc đối đỉnh)
∠ADH = ∠HBK (chứng minh trên)
Suy ra ∠DAH = ∠HKB
Mà ∠DAH = 90o nên ∠HKB = 90o
⇒ DC ⊥ BE (điều phải chứng minh)
Đúng 0
Bình luận (0)