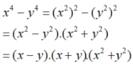=(x4−x3+2011x2)+

(x3−x2+2011x)+(x2−x+2011)

=x2(x2−x+2011)+x(x2−x+2011)+(x2−x+2011)

=(x2+x+1)(x2−x+2011)

=(x4−x3+2011x2)+(x3−x2+2011x)+(x2−x+2011)

=x2(x2−x+2011)+x(x2−x+2011)+(x2−x+2011)

=(x2+x+1)(x2−x+2011)

x3−x2+2011x)+(x2−x+2011)

=x2(x2−x+2011)+x(x2−x+2011)+(x2−x+2011)=(x2+x+1)(x2−x+2011)

x4 + 4

= (x2)2 + 22

= x4 + 2.x2.2 + 4 – 4x2

(Thêm bớt 2.x2.2 để có HĐT (1))

= (x2 + 2)2 – (2x)2

(Xuất hiện HĐT (3))

= (x2 + 2 – 2x)(x2 + 2 + 2x)

x4 – 2x2

(Có x2 là nhân tử chung)

= x2(x2 – 2)

Sửa đề: x^4+4y^4

=x^4+4x^2y^2+4y^4-4x^2y^2

=(x^2+2y^2)^2-4x^2y^2

=(x^2-2xy+2y^2)(x^2+2xy+2y^2)

Ta có:

x^4-y^4=(x^2-y^2)(x^2+y^2)=(x-y)(x+y)(x^2+y^2)

\(x^4+2010x^2+2009x+2010\)

\(=x^4-x+\left(2010x^2+2010x+2010\right)\)

\(=x\left(x^3-1\right)+2010\left(x^2+x+1\right)\)

\(=x\left(x-1\right)\left(x^2+x+1\right)+2010\left(x^2+x+1\right)\)

\(=\left(x^2+x+1\right)\left[x\left(x-1\right)+2010\right]=\left(x^2+x+1\right)\left(x^2-x+2010\right)\)

x 4 - 2 x 3 - 2 x 2 - 2 x - 3 =   ( x 4   −   1 )   −   ( 2 x 3   +   2 x 2 )   −   ( 2 x   +   2 ) =   ( x 2   +   1   ) ( x 2   −   1 )   −   2 x 2 ( x   +   1 )   − 2 ( x   +   1 ) =   ( x 2   +   1 ) ( x   −   1 ) ( x   +   1 )   −   2 x 2 ( x   +   1 )   − 2 ( x   +   1 ) =   ( x   +   1 ) ( x 2   +   1 ) ( x   −   1 )   −   2 x 2   –   2 =   ( x   +   1 ) (   x 2   +   1 ) ( x   −   1 )   −   2 ( x 2   +   1 ) =   ( x   +   1 ) (   x 2   +   1 ) ( x   –   1   −   2 ) =   ( x   +   1 ) (   x 2   +   1 ) ( x   −   3 )

x^4 - 2x^3 - 2x^2 - 2x - 3 

= x^4 - 1 - 2x^3 - 2x^2 - 2x -2 

= ( x - 1 ) ( x + 1 ) ( x^2 + 1 ) - 2x^2 ( x + 1 ) - 2 ( x + 1 ) 

= ( x + 1 ) [ ( x - 1 ) ( x^2 + 1 ) - 2x^2 - 2 ] 

= ( x + 1 ) [ ( x - 1 ) ( x^2 + 1 - 2 ( x^2 - 1 ) ] 

= ( x + 1 ) [ ( x - 1 ) ( x^2 + 1 ) - 2 ( x - 1 ) ( x + 1 ) ] 

= ( x + 1 ) ( x - 1 ) [ ( x^2 + 1 ) - 2 ( x +1 ) 

= ( x + 1 ) ( x - 1 ) ( x^2 +1 - 2x - 2 ) 

= ( x + 1 ) ( x - 1 ) ( x^2 - 2x - 1 ) 

d) x4 + 2x3 - 4x – 4 = (x4 – 4) + (2x3 – 4x) = (x2 – 2)(x2 + 2) + 2x(x2 – 2)

= (x2 – 2)(x2 + 2 + 2x) = (x - √2)( x + √2)( x2 + 2 + 2x)

e, x⁴ - 2x³ + x² 

= x²( x²  - 2x + 1)  

= x² (x - 1)²

e: \(x^4-2x^3+x^2\)

\(=x^2\cdot x^2-x^2\cdot2x+x^2\cdot1\)

\(=x^2\left(x^2-2x+1\right)\)

\(=x^2\left(x-1\right)^2\)

f: \(27y^3-x^3\)

\(=\left(3y\right)^3-x^3\)

\(=\left(3y-x\right)\left(9y^2+3xy+x^2\right)\)

\(e)x^4-2x^4+x^2 =x^2.x^2-2x.x^2+x^2+1 =(x^2)(x^2-2x+1) =x^2(x-1)^2 \)

\(f)27y^3-x^3 =(3y)^3-x^3 =(3y-3)(9y^2+3xy+x^2)\)