Cho hình chữ nhật ABCD. AB = 8cm, BC = 6cm. TÍNH BD = ?

Những câu hỏi liên quan
Cho hình chữ nhật coa AB = 8cm, AC = 10cm; AD =6cm. Tính BC; BD; DC.
Cho hình chữ nhật ABCD có AB = 8cm, BC = 6cm. Vẽ đường cao AH của tam giác ADB.a) Chứng minh ΔAHB đồng dạng với ΔBCD.b) Tính độ dài các cạnh BD, AH, DH.c) Tính điện tích ΔAHB.
Xem chi tiết
a) Xét ΔAHB vuông tại H và ΔBCD vuông tại C có
\(\widehat{ABH}=\widehat{BDC}\)(hai góc so le trong, AB//CD)
Do đó: ΔAHB∼ΔBCD(G-g)
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD có AB = 8cm , BC = 6cm , vẽ AH vuông góc với đường chéo BD ( H\(\in\) BD)
a) Tính độ dài dường cao AH
b) Chứng \(\Delta AHB\) \(\sim\) \(\Delta BCD\)
c) Chứng minh AD2 = DH . DB
a) Ta có :
AD = BC = 6 cm
Áp dụng hệ thức lượng trong tam giác ABD vuông tại A, ta có :
1/AD^2 + 1/AB^2 = 1/AH^2
<=> 1/6^2 + 1/8^2 = 1/AH^2
<=> AH = 4,8(cm)
b)
Áp dụng Pitago trong tam giác BCD vuông tại C có :
BC^2 + CD^2 = BD^2
<=> 6^2 + 8^2 = DB^2
<=> BD = 10(cm)
Xét hai tam giác vuông AHB và BCD có :
AH/BC = 4,8/6 = 4/5
AB/BD = 8/10 = 4/5
Do đó tam giác AHB đồng dạng với tam giác BCD
Đúng 2
Bình luận (1)
Cho hình chữ nhật ABCD có:
AB=8cm,BC=6cm
Gọi M là hình chiếu A trên BD
a, Chứng minh ∆HAD đồng dạng với ∆ ABD. Tính BC, HD
b, Chứng minh HA . BD= CD . AD
Dưới là ảnh hình vẽ của đề lm gig mk vs mk cần gấp
a. Xét hai tam giác vuông \(HAD\) và ABD có:
\(\left\{{}\begin{matrix}\widehat{DAH}=\widehat{DAB}\left(\text{cùng phụ }\widehat{ADB}\right)\\\widehat{DHA}=\widehat{DAB}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta HAD\sim\Delta ABD\) (g.g)
\(\Rightarrow\dfrac{HD}{AD}=\dfrac{AD}{BD}\Rightarrow HD=\dfrac{AD^2}{BD}\)
Áp dụng định lý Pitago: \(BD=\sqrt{AB^2+AD^2}=\sqrt{AB^2+BC^2}=\sqrt{8^2+6^2}=10\left(cm\right)\)
\(\Rightarrow HD=\dfrac{6^2}{10}=3,6\left(cm\right)\)
b.
Theo cmt, do hai tam giác HAD và ABD đồng dạng
\(\Rightarrow\dfrac{HA}{AB}=\dfrac{AD}{BD}\Rightarrow HA.BD=AB.AD\)
Mà ABCD là hcn \(\Rightarrow AB=CD\)
\(\Rightarrow HA.BD=CD.AD\) (đpcm)
Đúng 0
Bình luận (0)
cho hình chữ nhật ABCD có AB =8cm,BC =6cm , gọi H là chân đường vuông góc kẻ từ A xuống BD phân giác của góc BCD cắt BD ở E .
tính dt tứ giác AECH ?
giúp mình với mình cần gấp
Cho hình chữ nhật ABCD có AB=8cm, BC=6cm. Gọi I,K lần lượy là trung điểm của cạnh BC, AD. a) Tính diện tích hình bình hành AICK. b) Chung minh rằng ba đường AC, BD, IK cùng đi qua một điểm
a: BI=6/2=3cm
=>\(AI=\sqrt{8^2+3^2}=\sqrt{73}\left(cm\right)\)
\(S_{AICK}=\sqrt{73}\cdot3\left(cm^2\right)\)
b: AICK là hình bình hành
=>AC cắt IK tại trung điểm của mỗi đường(1)
ABCD là hbh
=>AC cắt BD tại trung điểm của mỗi đường(2)
Từ (1), (2) suy ra AC,IK,BD đồng quy
Đúng 0
Bình luận (0)
Tính diện tích và chu vi hình chữ nhật ABCD biết AB = 8cm, BC = 6cm
Chu vi hình chữ nhật ABCD là:
(8 + 6) × 2 = 28 (cm)
Diện tích hình chữ nhật ABCD là:
8 × 6 = 48 (cm2)
Đáp số: Chu vi: 28cm; Diện tích: 48cm2
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD AB=8cm AD=6cm Tính BD Hạ AH vuông góc với (H thuộc BD) chứng minh tam giác DHA đồng dạng với tam giác DAB Tính AH
a) Áp dụng định lí Pytago vào ΔABD vuông tại A, ta được:
\(BD^2=AB^2+AD^2\)
\(\Leftrightarrow BD^2=6^2+8^2=100\)
hay BD=10(cm)
b) Xét ΔDHA vuông tại H và ΔDAB vuông tại A có
\(\widehat{ADH}\) chung
Do đó: ΔDHA\(\sim\)ΔDAB(g-g)
Đúng 1
Bình luận (0)
Cho hình hộp chữ nhật ABCD. MNPQ có AB = 6cm; BC = 8cm và thể tích của hình hộp là 2 40 c m 3 . Tính AA’
A. 5cm
B. 6cm
C. 8cm
D. 10cm
Thể tích của hình hộp chữ nhật là
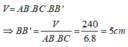
Suy ra: AA’ = BB’ =5cm
Chọn đáp án A
Đúng 0
Bình luận (0)
Cho hình chữ nhật abcd có ab=8cm, bc=6cm , gọi H là chân đường vuông góc từ a xuống bd.
Tia phân giác của góc BCD cắt bd ở e
a)CM △AHB ∞ △BCD
B) Tính tỉ số BE/ED
C) Tính tỉ số Sahb/ Sbcd
a: Xét ΔAHB vuông tại H và ΔBCD vuông tại C có
góc ABH=góc BDC
=>ΔAHB đồng dạng với ΔBCD
b: BE/EC=BC/CD=3/4
Đúng 0
Bình luận (0)





















