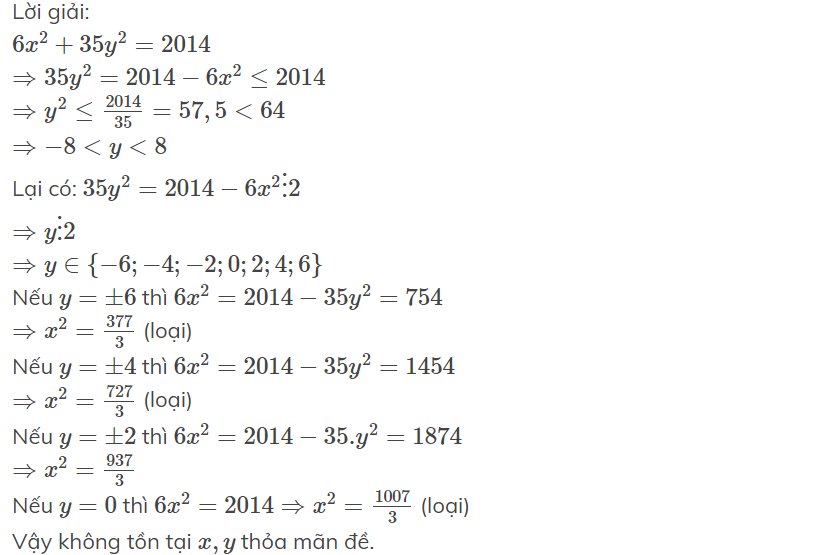6x^2 + 35y^2 =2014

Những câu hỏi liên quan
6x^2+35y^2=2014
tim x ; y thoa man 6x^2 + 35y^2 = 2014
m) 35y2 + 6x2 =2014
(x; y \(\in\)Z)
Ta có: 2014 là số chẵn
=> 35y2 + 6x2 là số chẵn
mà 6x2 là số chẵn => 35y2 là số chẵn (35y2\(\le\)2014)
=> y2 \(\in\){4; 16; 36}
=> y \(\in\){2; 4; 6}
Với y = 2 => 35.22 + 6x2 = 2014
=> 6x2 = 2014 - 140
=> 6x2 = 1874
=> x2 = 1874 : 6
=> x2 = 937/3 (ktm)
+) y = 4 => 35.42 + 6x2 = 2014
=> 6x2 = 2014 - 560
=> 6x2 = 1454
=> x2 = 1454 : 6
=> x2 = 727/3 (ktm)
+) y = 6 => 35.62 + 6x2 = 2014
=> 6x2 = 2014 - 1260
=> 6x2 = 754
=> x2 = 754 : 6
=> x2 = 377/3 (ktm)
Vậy ko có x;y (x;y \(\in\)Z) tm đề bài
tìm số TN x;y thỏa mản:6x^2+35y^2=2014
Tìm x,y nguyên dương: 6x^2+35y^2=2014
Lời giải:
$6x^2+35y^2=2014$
$\Rightarrow 35y^2=2014-6x^2\leq 2014$
$\Rightarrow y^2\leq \frac{2014}{35}=57,5< 64$
$\Rightarrow -8< y< 8$
Lại có: $35y^2=2014-6x^2\vdots 2$
$\Rightarrow y\vdots 2$
$\Rightarrow y\in\left\{-6; -4; -2; 0; 2; 4; 6\right\}$
Nếu $y=\pm 6$ thì $6x^2=2014-35y^2=754$
$\Rightarrow x^2=\frac{377}{3}$ (loại)
Nếu $y=\pm 4$ thì $6x^2=2014-35y^2=1454$
$\Rightarrow x^2=\frac{727}{3}$ (loại)
Nếu $y=\pm 2$ thì $6x^2=2014-35.y^2=1874$
$\Rightarrow x^2=\frac{937}{3}$
Nếu $y=0$ thì $6x^2=2014\Rightarrow x^2=\frac{1007}{3}$ (loại)
Vậy không tồn tại $x,y$ thỏa mãn đề.
Đúng 0
Bình luận (0)
Tìm x,y nguyên để 6x2+35y2=2014
tìm x;y ∈ N để 6x2+35y2=2014
TÌM SỐ TỰ NHIÊN X;Y:
6x2+35y2=2014
tìm số tự nhiên x y thỏa mãn 6x2 + 35y2 = 2014
Nhận xét: 6x2 và 2014 là số chẵn nên 35y2 cũng chẵn → y2 chẵn → y chẵn
Mặt khác: Từ 6x2 + 35y2 = 2014 nên 35y2 ≤ 2014 → y2 ≤ 58
Vậy y có thể nhận các giá trị: 0; 1; 2; 3; 4; 5; 6; 7.
Do y chẵn nên y có thể nhận các giá trị: 0; 2; 4; 6
Thay lần lượt các giá trị có thể nhận của y đề không tìm được giá trị của x.
Kết luận: Không tìm được các số tự nhiên x; y thoả mãn: 6x2 + 35y2 = 2014
Đúng 0
Bình luận (0)
cho mk hỏi
thay y kiểu j mak ko tìm đc giá trị của x
mak bài bảo tìm xy mak