cho nửa đường tròn (0;R)có đường kính AB .Vẽ bán kính OC vuông góc với AB.Trên cung BC lấy điểm M.Nối AM cắt OC ở E
a)chứng minh 4 điểm O,E,M,B cùng nằm trên một đường tròn
b)gọi H là trực tâm của tam giác OME chứng minh AOMH là hình thoi
c)các tia BM và OC cắt nhau ở F,các tia BE và AF cắt nhau tại K chứng minh H,K,M thẳng hàng
















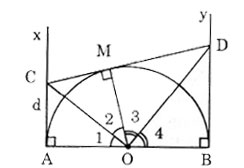 a) Ax ⊥ OA tại A, By ⊥ OB tại B nên Ax, By là các tiếp tuyến của đường tròn.
a) Ax ⊥ OA tại A, By ⊥ OB tại B nên Ax, By là các tiếp tuyến của đường tròn.







