Trên mặt phẳng toạ độ Oxy cho 3 điểm. điểm A có toạ độ 1;4, điểm B có toạ độ -3;-4, điểm C có toạ độ 1;0. Tính diện tích của tam giác ABC

Những câu hỏi liên quan
a) Tính khoảng cách từ gốc toạ độ C(0;0) đến điểm M(3 ; 4) trong mặt phẳng toạ độ Oxy.
b) Cho hai điểm I(a; b) và M(x ; y) trong mặt phẳng toạ độ Oxy. Nêu công thức tính độ dài đoạn thẳng IM.
a) Khoảng cách từ gốc tọa độ \(O\left( {0;0} \right)\) đến điểm \(M\left( {3;4} \right)\) trong mặt phẳng tọa độ Oxy là:
\(OM = \left| {\overrightarrow {OM} } \right| = \sqrt {{3^2} + {4^2}} = 5\)
b) Với hai điểm I(a; b) và M(x ; y) trong mặt phẳng toạ độ Oxy, ta có:\(IM = \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2}} \)
Đúng 0
Bình luận (0)
Trong mặt phẳng toạ độ Oxy cho đường thẳng (d1): y=-x+2 và (d2): y=1/4x
1. Vẽ (d1) và (d2) trên cùng hệ trục toạ độ Oxy
2. Lấy điểm B trên (d2) có hoành độ bằng -4. Viết phương trình đường thẳng (d3) song song với (d1) và qua điểm B
3. Tìm toạ độ giao điểm của (d1) và (d2) bằng phép tính
Xem chi tiết
Trong mặt phẳng toạ độ Oxy cho hàm số y=-2x+4 có đồ thị là đường thẳng (d).
a/Tìm toạ độ giao điểm của đường thẳng (d) với hai trục toạ đô
b/Tìm trên (d) điểm có hoành độ bằng tung độ
a, (d) cắt trục hoành tại A(xA;0) và trục tung B(0;xB)
Vì A thuộc (d) nên \(0=-2x_A+4\Leftrightarrow x_A=2 \Rightarrow A(2;0)\)
Vì B thuộc (d) nên \(y_B=-2.0+4=4\Rightarrow B(0;4)\)
Vậy A(2;0) và B(0;4) là hai điểm cần tìm.
b, Gọi C(xc;yc) là điểm có hoành độ bằng tung độ
⇒ xc = yc = a. Vì C thuộc (d) nên \(a=-2a+4\Leftrightarrow a=\dfrac{4}{3}\)
⇒ \(C(\dfrac{4}{3};\dfrac{4}{3})\) là điểm cần tìm.
Đúng 1
Bình luận (0)
Trên mặt phẳng toạ dộ Oxy, vẽ điểm A có toạ độ(3;4). Tính độ dài OA.
Trong mặt phẳng toạ độ Oxy, cho điểm M(-1; 3).
a) Tìm toạ độ điểm A đối xứng với điểm M qua gốc O.
b) Tìm toạ độ điểm B đối xứng với điểm M qua trục Ox.
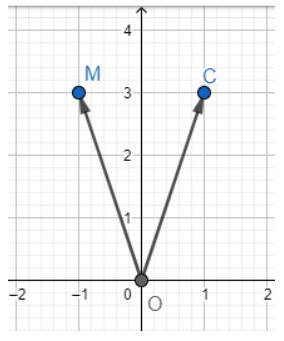
c) Tìm toạ độ điểm C đối xứng với điểm M qua trục Oy.
a) Dựa vào hình vẽ ta thấy \(A\left( {1; - 3} \right)\)
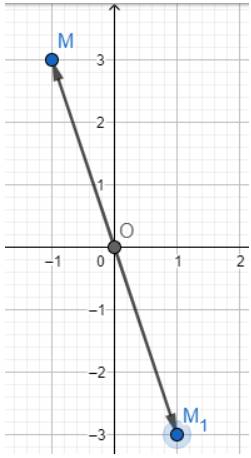
b) Dựa vào hình vẽ ta thấy \(B\left( { - 1; - 3} \right)\)

c) Dựa vào hình vẽ ta thấy \(C\left( {1;3} \right)\)
Đúng 0
Bình luận (0)
Trong mặt phẳng toạ độ Oxy, cho T là điểm trên trục tang có toạ độ là \(\left( {1;\sqrt 3 } \right)\) (Hình 5). Những điểm nào trên đường tròn lượng giác x có \(tanx = \sqrt 3 \)?Xác định số đo của các góc lượng giác đó.
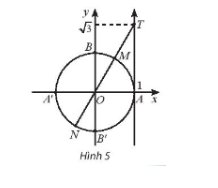
Những điểm biểu diễn góc x trên đường tròn lượng giác có \(tanx = \sqrt 3 \) là M và N.
Điểm M là điểm biểu diễn các góc lượng giác có số đo \(\frac{\pi }{3} + k2\pi ,k \in \mathbb{Z}\).
Điểm N là điểm biểu diễn các góc lượng giác có số đo \( - \frac{{2\pi }}{3} + k\pi ,k \in \mathbb{Z}\).
Đúng 0
Bình luận (0)
Trong mặt phẳng toạ độ Oxy, cho ba điểm A(2;3), B(-1; 1), C(3;- 1).
a) Tìm toạ độ điểm M sao cho\(\overrightarrow {AM{\rm{ }}} = {\rm{ }}\overrightarrow {BC} \).
b) Tìm toạ độ trung điểm N của đoạn thẳng AC. Chứng minh\(\overrightarrow {BN} {\rm{ }} = {\rm{ }}\overrightarrow {NM} \).
a) Gọi \(M\left( {a;b} \right) \Rightarrow \overrightarrow {AM} = \left( {a - 2;b - 3} \right)\)
Tọa độ vecto \(\overrightarrow {BC} = \left( {4; - 2} \right)\)
Để \(\overrightarrow {AM{\rm{ }}} = {\rm{ }}\overrightarrow {BC} \Leftrightarrow \left\{ \begin{array}{l}a - 2 = 4\\b - 3 = - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 6\\b = 1\end{array} \right.\)
Vậy để \(\overrightarrow {AM{\rm{ }}} = {\rm{ }}\overrightarrow {BC} \) thì tọa độ điểm M là:\(M\left( {6;1} \right)\)
b) Gọi \(N\left( {x,y} \right) \Rightarrow \overrightarrow {NC} = \left( {3 - x, - 1 - y} \right)\)và \(\overrightarrow {AN} = \left( {x - 2,y - 3} \right)\)
Do N là trung điểm AC nên \(\overrightarrow {AN} = \overrightarrow {NC} \Leftrightarrow \left\{ \begin{array}{l}x - 2 = 3 - x\\y - 3 = - 1 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{5}{2}\\y = 1\end{array} \right.\) . Vậy \(N\left( {\frac{5}{2},1} \right)\)
Ta có: \(\overrightarrow {BN} {\rm{ }} = \left( { \frac{7}{2};0} \right)\) và \(\overrightarrow {NM} = \left( {\frac{{ 7}}{2};0} \right)\). Vậy \(\overrightarrow {BN} {\rm{ }} = {\rm{ }}\overrightarrow {NM} \)
Đúng 0
Bình luận (0)
Trong mặt phẳng toạ độ Oxy, cho C là điểm trên trục côtang có toạ độ là (-1; 1) (Hình 7). Những điểm nào biểu diễn góc lượng giác x có \(cotx = - 1\)? Xác định số đo của các góc lượng giác đó.
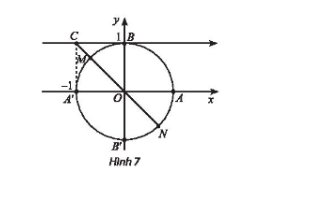
Trên đường tròn lượng giác hai điểm M và N biểu diễn các góc lượng giác có số đo góc x thỏa mãn \(cotx = - 1\).
Điểm M biểu diễn các góc lượng giác có số đo góc \(\frac{{3\pi }}{4} + k2\pi ,k \in \mathbb{Z}\).
Điểm N biểu diễn các góc lượng giác có số đo góc \( - \frac{\pi }{4} + k2\pi ,k \in \mathbb{Z}\).
Đúng 0
Bình luận (0)
Giúp mình với ạ, mình cảm ơn !
Trong mặt phẳng toạ độ Oxy cho điểm M nằm trên trục hoành có hoành độ bằng -1, toạ độ của điểm M là:
A. M(0;-1)
B. M(-1;0)
C. M(-1;-1)
D. M(-1;1)















