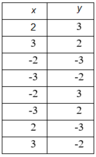
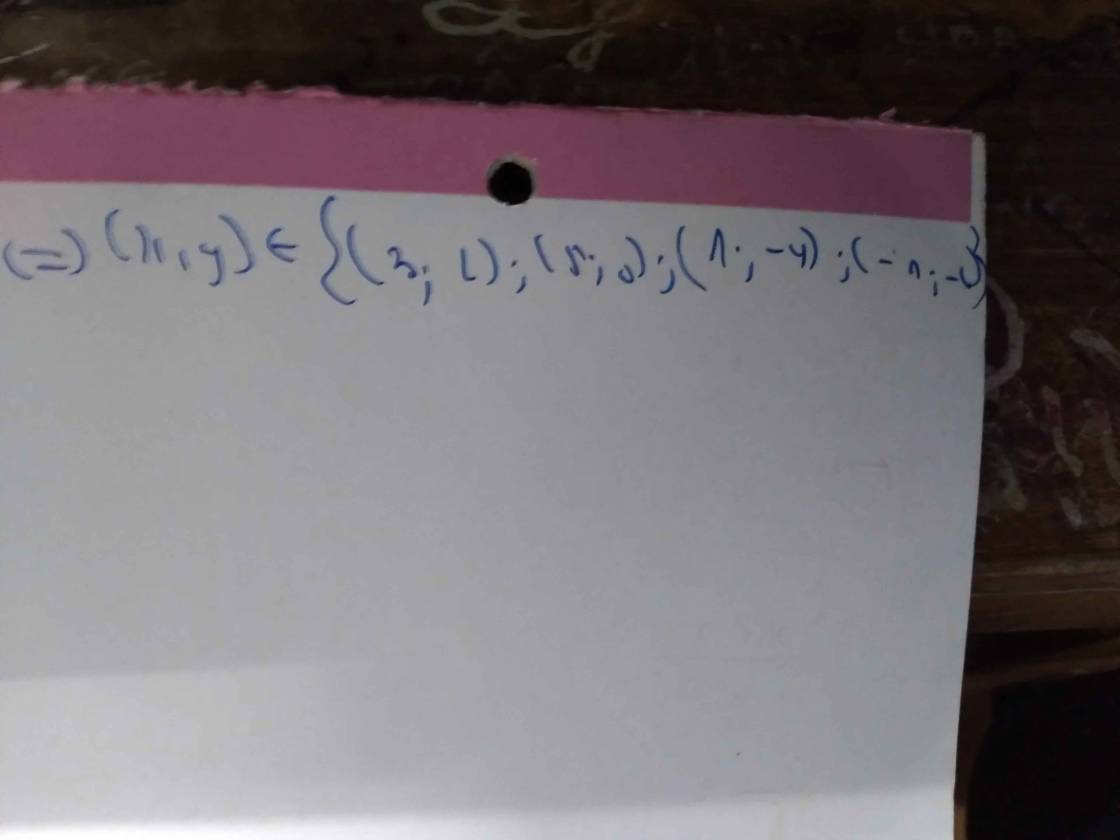Tìm các cặp (x;y) nguyên dương sao cho x<y và \(\sqrt{x}+\sqrt{y}=\sqrt{1980}\)

Những câu hỏi liên quan
a,Tìm x thuộc z/|x|<18
b,Tìm xy thuộc z/|x-3|+|y-5|=0
c,Tìm các cặp số nguyên (xy)/|x|+|y|=4
d,Tìm các cặp số nguyên (xy)/|x|+|y|<hoặc=3
Tìm x,y thuộc Z thỏa mãn 4x+5y=7 và trong các cặp số x,y tìm được hãy tìm cặp số x,y để M=5.|x|-3.|y| có giá trị nhỏ nhất
BÀi 1:Tìm các cặp số nguyên x,y biết 2x2+y2+xy=2(x+y)
Bài 2:Tìm các cặp số nguyên dương x,y biết x2+y2=3(x+y)
Bài 2: Giả sử tồn tại x,y nguyên dương t/m đề, khi đó pt cho tương đương:
\(4x^2+4y^2-12x-12y=0\Leftrightarrow\left(2x+3\right)^2+\left(2y+3\right)^2=18\)
Ta thấy: \(18=9+9=3^2+3^2\). Mà x,y thuộc Z+ nên \(\hept{\begin{cases}2x+3=3\\2y+3=3\end{cases}\Leftrightarrow}\hept{\begin{cases}x=0\\y=0\end{cases}}\)
Vậy cặp nghiệm nguyên t/m pt là (x;y) = (0;0)
Đúng 0
Bình luận (0)
Làm lại bài 2 :v (P/S: Bạn bỏ bài kia đi nhé)
\(4x^2+4y^2-12x-12y=0\Leftrightarrow\left(2x-3\right)^2+\left(2y-3\right)^2=18\)
Ta thấy: \(18=9+9=3^2+3^2\). Mà x,y thuộc Z+ nên \(\hept{\begin{cases}2x-3=3\\2y-3=3\end{cases}\Leftrightarrow}\hept{\begin{cases}x=3\\y=3\end{cases}}\)
Vậy (x;y) = (3;3)
Đúng 0
Bình luận (0)
Tìm các cặp số thỏa mãn...?
Tìm tât' cả các cặp số tự nhiên (x,y) biết x,y có 2 chữ số và thỏa mãn phương trình x^3 - y^2 = xy x^3-y^2=xy
=>(1) x(x^2-y)=y^2
x,y là các số tự nhiên => x^2-y là ước của y^2 => x^2 là ước của y^2 => x là ước của y => y=ax
=>(2) x^3=y(x+y)
=> x^3=ax(x+ax)=x^2.a.(a+1)
=> x=a(a+1)
Vậy x là tích 2 số tự nhiên liên tiếp; x,y có 2 chữ số.
a=1 => x=2 (loại)
a=2 => x=6 (loại)
a=3 => x=12 => y=36 (chọn)
a=4 => x=20 => y=80 (chọn)
a=5 => x=30 => y=150 (loại)
a>=5 thì y>100 => (loại)
Vậy (x,y)=(12,36) hoặc (x,y)=(20,80)
Đúng 0
Bình luận (1)
x^3-y^2=xy
=>(1) x(x^2-y)=y^2
x,y là các số tự nhiên => x^2-y là ước của y^2 => x^2 là ước của y^2 => x là ước của y => y=ax
=>(2) x^3=y(x+y)
=> x^3=ax(x+ax)=x^2.a.(a+1)
=> x=a(a+1)
Vậy x là tích 2 số tự nhiên liên tiếp; x,y có 2 chữ số.
a=1 => x=2 (loại)
a=2 => x=6 (loại)
a=3 => x=12 => y=36 (chọn)
a=4 => x=20 => y=80 (chọn)
a=5 => x=30 => y=150 (loại)
a>=5 thì y>100 => (loại)
Vậy (x,y)=(12,36) hoặc (x,y)=(20,80)
Đúng 0
Bình luận (0)
tìm các cặp sô nguyên x,y

=>x(y-2)-2y+4=4
=>(x-2)(y-2)=4
=>(x-2;y-2) thuộc {(1;4); (4;1); (2;2); (-2;-2); (-4;-1); (-1;-4)}
=>(x,y) thuộc {(3;5); (5;3); (4;4); (0;0); (-2;1); (1;-2)}
Đúng 2
Bình luận (0)
Tìm các cặp số nguyên x, y biết x + y = 5
a) Tìm cặp số x,y nguyên dương thỏa mãn \(x^2+y^2\left(x-y+1\right)-\left(x-1\right)y=22\)
b) Tìm các cặp số x,y,z nguyên dương thỏa mãn \(\dfrac{xy+yz+zx}{x+y+z}=4\)
tìm các cặp số nguyên (x,Y) thoarmanx xy+x-2y=5
tìm các cặp x,y nguyên sao cho
2xy+x-2y=4
\(2xy+x-2y=4\\\Rightarrow (2xy+x)-2y-1=3\\\Rightarrow x(2y+1)-(2y+1)=3\\\Rightarrow (2y+1)(x-1)=3\)
Ta có: \(x,y\) nguyên
\(\Rightarrow2y+1;x-1\) là các ước của \(3\)
Mặt khác: \(2y+1\) là số lẻ với mọi \(y\) nguyên
Ta có bảng:
| x - 1 | 3 | -3 |
| 2y + 1 | 1 | -1 |
| x | 4 | -2 |
| y | 0 | -1 |
(thoả mãn điều kiện \(x,y\) nguyên)
Vậy: ...
#\(Toru\)
Đúng 1
Bình luận (0)
Tìm các cặp số x,y:
x+2y=10
Có rất nhiềm cặp số x và y vì bạn không hạn chế x;y \(\in\)N hay Q
Đúng 0
Bình luận (0)