Câu b,d,f,h


Những câu hỏi liên quan
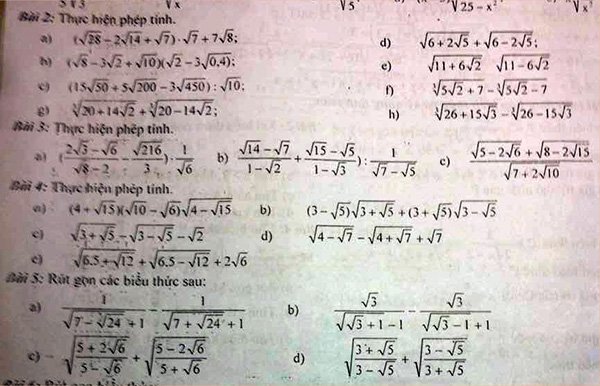
Làm giùp em bài 2 câu b, c, g, d, e, f, h
Bài 2:
d) Ta có: \(\sqrt{6+2\sqrt{5}}+\sqrt{6-2\sqrt{5}}\)
\(=\sqrt{5}+1+\sqrt{5}-1\)
\(=2\sqrt{5}\)
e) Ta có: \(\sqrt{11+6\sqrt{2}}-\sqrt{11-6\sqrt{2}}\)
\(=3+\sqrt{2}-3+\sqrt{2}\)
\(=2\sqrt{2}\)
Đúng 0
Bình luận (1)
Cho các đa thức: f(x)+=4x^3-x^2+2x-5 g(x)=3x^3+2x^2-x-5 h(x)= -3x^3+x^2-2x+4
a)Tính f(x)+g(x)-h(x); f(x)-[g(x)-h(x)]
b)Tính f(0); g(1/2); h(-1)
c)x=-1 có là nghiệm của f(x) không? Vì sao?
d) Tìm x để f(x)=g(x)
Giúp mình câu c và câu d...Cảm ơn...!!!
c) thay x=1 vào đa thức f(x) ta có: f(1)=4.1^3-1^2+2.1-5
=4-2+2-5
=- 1
vậy 1 k phải là nghiệm của đa thức f(x)
MÌNH CHỈ LÀM ĐƯỢC C THÔI HOK TỐT
Đúng 0
Bình luận (0)
làm sai nha chỗ nào là 1 thì thay bằng -1 nha kq sẽ ra nha
Đúng 0
Bình luận (0)
a) \(f\left(x\right)+g\left(x\right)-h\left(x\right)\)
\(=\left(4x^3-x^2+2x-5\right)+\left(3x^3+2x^2-x-5\right)-\left(-3x^3+x^2-2x+4\right)\)
\(=4x^3-x^2+2x-5+3x^3+2x^2-x-5+3x^3-x^2+2x-4\)
\(=\left(4x^3+3x^3+3x^3\right)-\left(x^2+x^2-2x^2\right)+\left(2x-x+2x\right)-\left(5+5+4\right)\)
\(=10x^3-0+3x-14\)
\(=10x^3+3x-14\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Ai giúp mình câu này với:
Có 8 chữ cái từ A đến H. Mỗi một trong tám chữ cái đều khác nhau
số từ 1 đến 8.
A + B + C = F + G + H = 12. D + E = 12. C + D + E + F = 26. D = 5, H = 1. A, B,
và C là các con số. Tìm giá trị của mỗi chữ cái.
A,B,C,F,G,H,D,E
Dấu . là nhân nha
Câu 1: ( 3,0 điểm )a. Xác định A, B, M, D, E, F, G, H, I, K, L và hoàn thành các phương trình hoá học sau:1. FeS2 + O2 - A + B2. A + O2 - M3. M + D - axit E4. E + Cu - F + A + D5. A + D - axit G6. G + KOH - H + D7. H + Cu(NO3)2 - I + K8. I + E - F + A + D9. A + Cl2 + D - E + Lb. Hòa tan một lượng oxit của kim loại R vào dung dịch H2SO4 4,9% ( vừa đủ ) thì thu được một dung dịch muối có nồng độ 5,87%. Xác định CTPT của oxit kim loạ
Đọc tiếp
Câu 1: ( 3,0 điểm )
a. Xác định A, B, M, D, E, F, G, H, I, K, L và hoàn thành các phương trình hoá học sau:
1. FeS2 + O2 -> A + B
2. A + O2 -> M
3. M + D -> axit E
4. E + Cu -> F + A + D
5. A + D -> axit G
6. G + KOH -> H + D
7. H + Cu(NO3)2 -> I + K
8. I + E -> F + A + D
9. A + Cl2 + D -> E + L
b. Hòa tan một lượng oxit của kim loại R vào dung dịch H2SO4 4,9% ( vừa đủ ) thì thu được một dung dịch muối có nồng độ 5,87%. Xác định CTPT của oxit kim loạ
Giúp câu d . e . f . g . h
\(2,\\ a,x=36\Leftrightarrow P=\dfrac{6+1}{6-2}=\dfrac{7}{4}\\ b,x=6-2\sqrt{5}\Leftrightarrow\sqrt{x}=\sqrt{5}-1\\ \Leftrightarrow P=\dfrac{\sqrt{5}-1+1}{\sqrt{5}-1-2}=\dfrac{\sqrt{5}}{\sqrt{5}-3}=\dfrac{5-3\sqrt{5}}{2}\\ c,x=\dfrac{2}{2+\sqrt{3}}=4-2\sqrt{3}\Leftrightarrow\sqrt{x}=\sqrt{3}-1\\ \Leftrightarrow P=\dfrac{\sqrt{3}-1+1}{\sqrt{3}-1-2}=\dfrac{\sqrt{3}}{\sqrt{3}-3}=\dfrac{3\left(\sqrt{3}+1\right)}{-6}=\dfrac{-\sqrt{3}-1}{2}\)
Đúng 1
Bình luận (1)
h: Ta có: \(x-7\sqrt{x}+10=0\)
nên x=25
Thay x=25 vào P, ta được:
\(P=\dfrac{5+1}{5-2}=\dfrac{6}{3}=2\)
Đúng 0
Bình luận (0)
cần gấp ạ câu d , e , f, g, h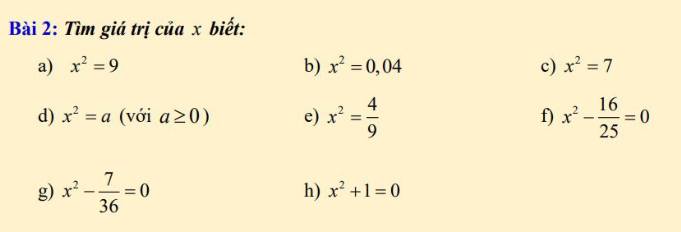
d) \(x^2=a\left(a\ge0\right)\)
\(\Rightarrow x=\sqrt{a}\)
e) \(x^2=\dfrac{4}{9}\)
\(\Rightarrow x^2=\left(\pm\dfrac{2}{3}\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{2}{3}\end{matrix}\right.\)
f) \(x^2-\dfrac{16}{25}=0\)
\(\Rightarrow x^2=\dfrac{16}{25}\)
\(\Rightarrow x^2=\left(\pm\dfrac{4}{5}\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{4}{5}\\x=-\dfrac{4}{5}\end{matrix}\right.\)
g) \(x^2-\dfrac{7}{36}=0\)
\(\Rightarrow x^2=\dfrac{7}{36}\)
\(\Rightarrow x^2=\left(\pm\sqrt{\dfrac{7}{36}}\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}x=\sqrt{\dfrac{7}{36}}\\x=-\sqrt{\dfrac{7}{36}}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{7}}{6}\\x=-\dfrac{\sqrt{7}}{6}\end{matrix}\right.\)
h) Ta có: \(x^2\ge0\forall x\)
\(\Rightarrow x^2+1\ge1>0\forall x\)
mà \(x^2+1=0\)
nên không tìm được giá trị nào của x thoả mãn đề bài.
Đúng 2
Bình luận (0)
Câu 2: Viết các PTPU (nếu có) a. Al2O3 + HCl → b. Fe2O3 + SO3 → c. Na2O + H2O → d. Fe3O4 + HCl → Câu 3: e. SO3 + H2O→ f. NaOH(dư) + CO2 → g. P2O5 + H2O→ h. CaO + CO2 →
\(a,Al_2O_3+6HCl\rightarrow2AlCl_3+3H_2O\\ b,Fe_2O_3+SO_3\rightarrow Không.p.ứ\\ c,Na_2O+H_2O\rightarrow2NaOH\\ d,Fe_3O_4+8HCl\rightarrow2FeCl_3+FeCl_2+4H_2O\\ e,SO_3+H_2O\rightarrow H_2SO_4\\ f,2NaOH\left(dư\right)+CO_2\rightarrow Na_2CO_3+H_2O\\ g,P_2O_5+3H_2O\rightarrow2H_3PO_4\\ h,CaO+CO_2\rightarrow CaCO_3\)
Đúng 2
Bình luận (0)
Câu 2: Tìm 1,2,3 chữ số tận cùng của:
a) 20132014 . b) 20142015. c) 20152016. d) . e) . f) g). h)

Chỉ giải hộ em câu : C , D , E , F , G , H ạ ;-; !
a: Ta có: \(\sqrt{75}-\sqrt{5\dfrac{1}{3}}+\dfrac{9}{2}\sqrt{2\dfrac{2}{3}}+2\sqrt{27}\)
\(=5\sqrt{3}+\dfrac{4}{3}\sqrt{3}+3\sqrt{6}+6\sqrt{3}\)
\(=\dfrac{37}{3}\sqrt{3}+3\sqrt{6}\)
c: Ta có: \(\left(\sqrt{12}+2\sqrt{27}\right)\cdot\dfrac{\sqrt{3}}{2}-\sqrt{150}\)
\(=\left(2\sqrt{3}+6\sqrt{3}\right)\cdot\dfrac{\sqrt{3}}{2}-5\sqrt{6}\)
\(=12-5\sqrt{6}\)
Đúng 0
Bình luận (1)
giúp mình câu d, e,f, h đi ạ, mình cảm ơn
\(e,=\dfrac{\left(3+\sqrt{2}\right)\left(2\sqrt{2}+1\right)}{7}-\sqrt{\dfrac{\left(\sqrt{2}+1\right)^2}{\left(\sqrt{2}-1\right)\left(\sqrt{2}+1\right)}}\\ =\dfrac{7\sqrt{2}+7}{7}-\dfrac{\sqrt{2}+1}{1}=\sqrt{2}+1-\sqrt{2}-1=0\)
\(f,=\sqrt{\dfrac{\left(2\sqrt{3}-3\right)^2}{\left(2\sqrt{3}-3\right)\left(2\sqrt{3}+3\right)}}\left(2+\sqrt{3}\right)\\ =\dfrac{\left(2\sqrt{3}-3\right)\left(2+\sqrt{3}\right)}{\sqrt{3}}\\ =\dfrac{\sqrt{3}}{\sqrt{3}}=1\)
\(h,=\sqrt{\dfrac{\left(3\sqrt{5}-1\right)\left(2\sqrt{5}-3\right)}{20-9}}\left(\sqrt{2}+\sqrt{10}\right)\\ =\sqrt{\dfrac{2\left(33-11\sqrt{5}\right)}{11}}\left(\sqrt{5}+1\right)\\ =\sqrt{\dfrac{22\left(3-\sqrt{5}\right)}{11}}\left(\sqrt{5}+1\right)\\ =\sqrt{6-2\sqrt{5}}\left(\sqrt{5}+1\right)=\left(\sqrt{5}-1\right)\left(\sqrt{5}+1\right)=4\)
Đúng 4
Bình luận (0)





















