Tìm đạo hàm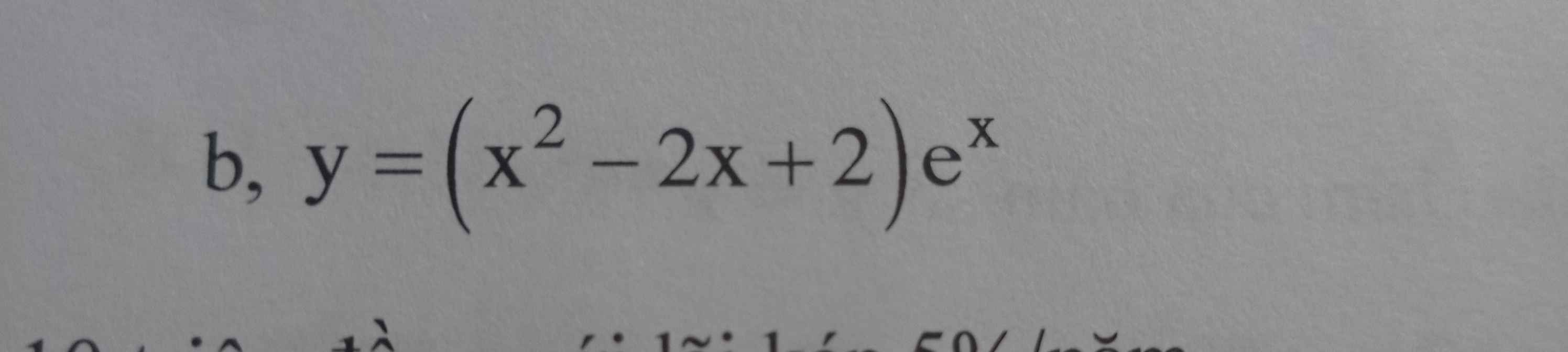
Những câu hỏi liên quan
từ nguyên hàm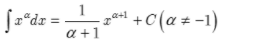 
tìm đạo hàm hàm số
Tìm đạo hàm của hàm số nào vậy nhỉ bạn?
Đúng 0
Bình luận (0)
SGK Chân trời sáng tạo
20 tháng 8 2023 lúc 20:05
a) Dùng định nghĩa tỉnh đạo hàm của hàm số \(y = x\) tại điểm \(x = {x_0}\).
b) Nhắc lại đạo hàm của các hàm số \(y = {x^2},y = {x^3}\) đã tìm được ở bài học trước. Từ đó, dự đoán đạo hàm của hàm số \(y = {x^n}\) với \(n \in {\mathbb{N}^*}\).
a) Với bất kì \({x_0} \in \mathbb{R}\), ta có:
\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{x - {x_0}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} 1 = 1\)
Vậy \(f'\left( x \right) = {\left( x \right)^\prime } = 1\) trên \(\mathbb{R}\).
b) Ta có:
\(\begin{array}{l}{\left( {{x^2}} \right)^\prime } = 2{\rm{x}}\\{\left( {{x^3}} \right)^\prime } = 3{{\rm{x}}^2}\\...\\{\left( {{x^n}} \right)^\prime } = n{{\rm{x}}^{n - 1}}\end{array}\)
Đúng 0
Bình luận (0)
Tìm đạo hàm của hàm số
y
x
e
x
A.
y
1
+
e
x
B.
y
1
+
x
e
x
C.
y
e
x
D.
y
x
....
Đọc tiếp
Tìm đạo hàm của hàm số y = x e x
A. y ' = 1 + e x
B. y ' = 1 + x e x
C. y ' = e x
D. y ' = x . e x
Tìm đạo hàm của hàm số
y
x
x
x
A.
y
7
8
x
8
B.
y
7
8
x
1
8
C.
y
3
8...
Đọc tiếp
Tìm đạo hàm của hàm số y = x x x
A. y ' = 7 8 x 8
B. y ' = 7 8 x 1 8
C. y ' = 3 8 x 5 8
D. y ' = 5 4 x 4
Viết lại hàm số dưới dạng lũy thừa
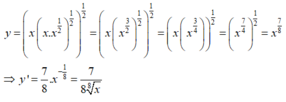
Đáp án A.
Đúng 0
Bình luận (0)
Tìm đạo hàm của hàm số
y
x
x
x
3
3
3
A.
y
5
12
x
-
7
12
B.
y
1...
Đọc tiếp
Tìm đạo hàm của hàm số y = x x x 3 3 3
A. y ' = 5 12 x - 7 12
B. y ' = 1 x x x 3 3 3 2 3
C. y ' = 13 27 x - 14 12
D. y ' = 1 9 x - 8 9
Tìm đạo hàm của hàm số
y
3
x
.
e
x
A.
x
.
(
3
e
)
x
-
1
B.
3
x
e
x
l
n
(
3
+
e
)
C.
3
x...
Đọc tiếp
Tìm đạo hàm của hàm số y = 3 x . e x
A. x . ( 3 e ) x - 1
B. 3 x e x l n ( 3 + e )
C. 3 x e x ( l n 3 + l n 1 )
D. 3 x e x ( l n 3 + 1 )
Tìm đạo hàm của hàm số ylogx. A. y
1
x
B. y
ln
10
x
C. y
1
x
ln
10
D. y
1
10
ln
x
Đọc tiếp
Tìm đạo hàm của hàm số y=logx.
A. y' = 1 x
B. y' = ln 10 x
C. y' = 1 x ln 10
D. y' = 1 10 ln x
Tìm đạo hàm của hàm số
y
log
x
2
+
x
.
A.
y
2
x
+
1
x
2
+...
Đọc tiếp
Tìm đạo hàm của hàm số y = log x 2 + x .
A. y ' = 2 x + 1 x 2 + x log 10 .
B. y ' = 2 x + 1 ln 10 .
C. y ' = 2 x + 1 x 2 + x ln 10 .
D. y ' = 1 x 2 + x ln 10 .
Tìm đạo hàm của hàm số
y
x
5
+
4
x
5
A.
y
1
5
x
4
5
+
10
x
3
B.
y
1
2
x
5...
Đọc tiếp
Tìm đạo hàm của hàm số y = x 5 + 4 x 5
A. y ' = 1 5 x 4 5 + 10 x 3
B. y ' = 1 2 x 5 + 10 x 4 x 5
C. y ' = 1 5 x 4 5 + 10 x 3
D. y ' = 1 2 x 5 + 2 x 5
Tìm đạo hàm của hàm số
y
log
2
2
x
+
1
.
A.
y
2
2
x
+
1
.
B.
y
1...
Đọc tiếp
Tìm đạo hàm của hàm số y = log 2 2 x + 1 .
A. y ' = 2 2 x + 1 .
B. y ' = 1 2 x + 1 .
C. y ' = 1 2 x + 1 ln 2 .
D. y ' = 2 2 x + 1 ln 2 .
Đáp án là D
Ta có: y ' = 2 x + 1 ' 2 x + 1 . ln 2 = 2 2 x + 1 . ln 2
Đúng 0
Bình luận (0)