Tìm nghiệm nguyên của phương trình:
3x2 + 5y2 = 345
Những câu hỏi liên quan
Tìm nghiệm nguyên của phương trình: 4x2+ 5y2 = 2022
\(4x^2+5y^2=2022\) (1)
-Vì \(4x^2⋮2\) và \(2022⋮2\) nên \(5y^2⋮2\Rightarrow y^2⋮2\Rightarrow y⋮2\)
-Đặt \(y=2k\left(k\in Z\right)\) và thay vào (1) ta được:
\(4x^2+5.\left(2k\right)^2=2022\)
\(\Leftrightarrow4x^2+5.4k^2=2022\)
\(\Leftrightarrow4x^2+20k^2=2022\)
\(\Leftrightarrow x^2+5k^2=\dfrac{2022}{4}=505.5\) (vô lý do x,k là các số nguyên)
-Vậy phương trình vô nghiệm.
Đúng 0
Bình luận (0)
Tìm nghiệm nguyên của phương trình: 3x2 + 13xy + 26(x − y) + 39y2 = 2022
Tìm nghiệm nguyên của phương trình 3.x2+5y2=345.
Bài 1 : tìm x ; y nguyên dương
2xy + x + y = 83
Bài 2 tìm nghiệm nguyên của phương trình :
a ) x2 + 2y2 + 3xy - x - y + 3 = 0
b ) 6x2y3 + 3x2 - 10y3 = -2
bài 1
Ta có 2xy+x+y=83
<=>4xy+2x+2y=166
2x*(2y+1)+(2y+1)=167
(2x+1)*(2y+1)=167
=>2x+1;2y+1 thuộc Ư(167)
do x,y nguyên dương =>2TH
TH1 2x+1=1;2y+1=167=>x=...;y=....
TH2 2x+1=167;2y+1=1=>x=...;y=....
Đúng 0
Bình luận (0)
Cho phương trình 3x2-c=a(x2-2x+1)-b(x-1) tìm 3 số nguyên a,b,c để phương trình có nghiệm với mọi x thược R.
=>3x^2-c=ax^2-2ax+a-bx+b
=>3x^2-c-a*x^2+2ax-a+bx-b=0
=>x^2(3-a)+x(2a+b)-a-b-c=0
Để phương trình luôn có nghiệm thì 3-a=0 và 2a+b=0 và a+b+c=0
=>a=3; b=-6; c=-a-b=-3+6=3
Đúng 0
Bình luận (1)
Cho đa thức: Q(x) = x4 + 3x2 + 1
a. Phân tích đa thức Q(x) thành nhân tử.
b. Tìm nghiệm nguyên của phương trình y2 = x4 + 3x2 + 1.
\(3x^2+4x+1=3x^2+3x+x+1=\left(x+1\right)\left(3x+1\right)\)
Đúng 0
Bình luận (0)
Tìm tập nghiệm của phương trình
3
x
2
+
2
x
1
. A.
S
-
1
;
3
B.
S
0
;
-
2
C.
S...
Đọc tiếp
Tìm tập nghiệm của phương trình 3 x 2 + 2 x = 1 .
A. S = - 1 ; 3
B. S = 0 ; - 2
C. S = 1 ; - 3
D. S = 0 ; 2
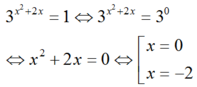
Vậy tập nghiệm của phương trình là S = 0 ; - 2
Chọn B.
Đúng 0
Bình luận (0)
Tìm tập nghiệm của phương trình 3 x 2 + 2 x = 1 .
A.S={-1;3}
B. S = {0;2}
C. S = {1;-3}
D. S = {0;2}
Tìm tập nghiệm S của phương trình
3
x
2
4
x
A.
0
B.
0
;
log
3
4
C.
0
;
log
4...
Đọc tiếp
Tìm tập nghiệm S của phương trình 3 x 2 = 4 x
A. 0
B. 0 ; log 3 4
C. 0 ; log 4 3
D. 0 ; log 9 4