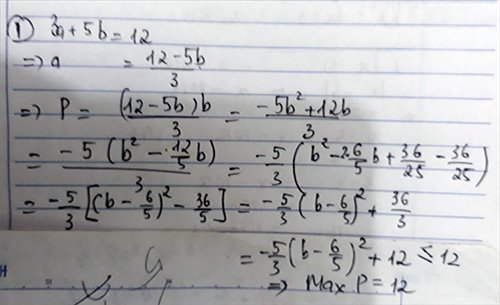Tìm max của \(\frac{x}{\left(x+2016\right)^2}\)

Những câu hỏi liên quan
T ÌM GIÁ trị của x thoả mãn: |2x+3|+|2x-1|=\(\frac{8}{3\left(x+1\right)^2+2}\)
Ta có: \(\left|2x+3\right|+\left|2x-1\right|=\left|2x+3\right|+\left|1-2x\right|\ge\left|2x+3+1-2x\right|=4\)
=> \(\left|2x+3\right|+\left|2x-1\right|\ge4\)(1)
Ta lại có: \(\frac{8}{3\left(x+1\right)^2+2}\le\frac{8}{2}=4\)
=> \(\left|2x+3\right|+\left|2x-1\right|\ge4\) (2)
Từ (1); (2) : \(\left|2x+3\right|+\left|2x-1\right|=\frac{8}{3\left(x+1\right)^2+2}\)
<=> \(\hept{\begin{cases}\left(2x+3\right)\left(1-2x\right)\ge0\\\left(x+1\right)^2=0\end{cases}\Leftrightarrow x=-1}\)(TM)
Vậy:...
a) A=\(\frac{-6}{2016-\left|x\right|}\)
b) B=\(\frac{-6}{\left|x\right|+2016}\)
max , min
a) Ta có : \(-\left|x\right|\le0\Leftrightarrow-\left|x\right|+2016\le2016\Leftrightarrow\frac{1}{2016-\left|x\right|}\ge\frac{1}{2016}\Leftrightarrow\frac{-6}{2016-\left|x\right|}\le-\frac{6}{2016}=-\frac{1}{336}\)
Dấu "=" xảy ra khi x = 0
Max A = \(-\frac{1}{336}\Leftrightarrow x=0\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho a,b,c >0; biết \(\hept{\begin{cases}a^2=b+4032\\x+y+z=a\\x^2+y^2+z^2=b\end{cases}}\)
\(P=x\sqrt{\frac{\left(2016+y^2\right)\left(2016+z^2\right)}{2016+x^2}}+y\sqrt{\frac{\left(2016+z^2\right)\left(2016+x^2\right)}{\left(2016+y^2\right)}}+z\sqrt{\frac{\left(2016+x^2\right)\left(2016+y^2\right)}{\left(2016+z^2\right)}}\)
Chứng minh giá trị của P không phụ thuộc vào x,y,z
Bạn thêm điều kiện x,y,z lớn hơn 0 nhé :)
Từ giả thiết ta suy ra : \(a^2=b+4032\Rightarrow\left(x+y+z\right)^2=x^2+y^2+z^2+4032\)
\(\Rightarrow xy+yz+zx=2016\)thay vào :
\(x\sqrt{\frac{\left(2016+y^2\right)\left(2016+z^2\right)}{2016+x^2}}=x\sqrt{\frac{\left(y^2+xy+yz+zx\right)\left(z^2+xy+yz+zx\right)}{x^2+xy+yz+zx}}\)
\(=x\sqrt{\frac{\left(x+y\right)\left(y+z\right)\left(z+y\right)\left(z+x\right)}{\left(x+y\right)\left(x+z\right)}}=x\sqrt{\left(y+z\right)^2}=x\left|y+z\right|=xy+xz\)vì x,y,z > 0
Tương tự : \(y\sqrt{\frac{\left(2016+z^2\right)\left(2016+x^2\right)}{2016+y^2}}=xy+zy\)
\(z\sqrt{\frac{\left(2016+x^2\right)\left(2016+y^2\right)}{2016+z^2}}=zx+zy\)
Suy ra \(P=2\left(xy+yz+zx\right)=2.2016=4032\)
Đúng 0
Bình luận (0)
x,y dương x+y=2. Max
T=\(\sqrt{1+\frac{1}{x}+\frac{1}{\left(x+1\right)^2}}+\sqrt{1+\frac{1}{y}+\frac{1}{\left(y+1\right)^2}}\) +\(\frac{4}{\left(x+1\right)\left(y+1\right)}\)
Sửa đề: \(T=\sqrt{1+\frac{1}{x^2}+\frac{1}{\left(x+1\right)^2}}+\sqrt{1+\frac{1}{y^2}+\frac{1}{\left(y+1\right)^2}}+\frac{4}{\left(x+1\right)\left(x+1\right)}\)
Rồi để ý: \(1+\frac{1}{x^2}+\frac{1}{\left(x+1\right)^2}=\left[\frac{1}{x}-\frac{1}{\left(x+1\right)}\right]^2+\frac{2}{x\left(x+1\right)}+1\)
\(=\left[\frac{1}{x\left(x+1\right)}\right]^2+\frac{2}{x\left(x+1\right)}+1=\left[\frac{1}{x\left(x+1\right)}+1\right]^2=\left[1+\frac{1}{x}-\frac{1}{x+1}\right]^2\)
Tương tự với y rồi thế vào căn là xong:D
Tìm x biết\(\frac{1}{x\left(x+1\right)}+\frac{1}{\left(x+1\right)\left(x+2\right)}+\frac{1}{\left(x+2\right)\left(x+3\right)}+...+\frac{1}{\left(x+2015\right)\left(x+2016\right)}=\frac{1}{x+2016}\)
\(\frac{1}{x\left(x+1\right)}+\frac{1}{\left(x+1\right)\left(x+2\right)}+\frac{1}{\left(x+\right)\left(x+3\right)}+...+\frac{1}{\left(x+2015\right)\left(x+2016\right)}=\frac{1}{x+2016}\)
\(\frac{1}{x}-\frac{1}{x+1}+\frac{1}{x+1}-\frac{1}{x+2}+\frac{1}{x+2}-\frac{1}{x+3}+...+\frac{1}{x+2015}-\frac{1}{x+2016}=\frac{1}{x+2016}\)
\(\frac{1}{x}-\frac{1}{x+2016}=\frac{1}{x+2016}\)
\(\frac{1}{x}-\frac{1}{x+2016}-\frac{1}{x+2016}=0\)
\(\frac{1}{x}-\frac{2x}{x+2016}=0\)
\(\frac{x+2016}{x\left(x+2016\right)}-\frac{2x}{x\left(x+2016\right)}=0\)
\(\frac{x+2016-2x}{x\left(x+2016\right)}=0\Leftrightarrow2016-x=0\Leftrightarrow x=2016\)
Đúng 0
Bình luận (0)
Tìm Max A = \(\frac{x}{\left(x+2016\right)^2}\)
Mink sẽ tic-k cho
Cho \(x,y,z\in\left[2018,2019\right]\)
Tìm max của \(f\left(x,y,z\right)=\frac{\left|2018.2019-xy\right|}{\left(x+y\right)z}+\frac{\left|2018.2019-yz\right|}{\left(y+z\right)x}+\frac{\left|2018.2019-zx\right|}{\left(z+x\right)y}\)
tìm max của C\(_{\left(x\right)}\)=\(\frac{\frac{7}{2}\left(2x-3\right)+\frac{21}{2}-8}{2x-3}\)
1.tìm max A(frac{x}{x+2020})^2 với x0
2. tìm min C frac{left(4x+1right)left(4+xright)}{x} với x dương
3.cho 3a+5b12. tìmmin Bab
4.tìm min x^2-x+4+frac{1}{x^2-x}
5. cho x,y là 2 số thỏa mãn 2x^2+frac{1}{x^2}+frac{y}{4}4.tìm min max của xy
6. cho a,b0 và a+b1. tìm min Mleft(1+frac{1}{a}right)^2left(1+frac{1}{b}right)^2
Đọc tiếp
1.tìm max A=(\(\frac{x}{x+2020}\))\(^2\) với x>0
2. tìm min C= \(\frac{\left(4x+1\right)\left(4+x\right)}{x}\) với x dương
3.cho 3a+5b=12. tìmmin B=ab
4.tìm min \(x^2-x+4+\frac{1}{x^2-x}\)
5. cho x,y là 2 số thỏa mãn \(2x^2+\frac{1}{x^2}+\frac{y}{4}=4\).tìm min max của xy
6. cho a,b>0 và a+b=1. tìm min M=\(\left(1+\frac{1}{a}\right)^2\left(1+\frac{1}{b}\right)^2\)