không tính kết quả hãy so sánh A và B
A=m*(n+1)
B=n*(m+n)
Không tính kết quả cụ thể , hãy so sánh biểu thức A và B
a, A=abc+pq +425 ; B= 4ab + 5q + aq2
b, A= m x ( n+1) ; B = n x (m + 1) Với m>n
c, A= 28x6x30 ; B = 29x6x29
ho biết 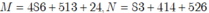 . Không tính kết quả hãy so sánh M, N
. Không tính kết quả hãy so sánh M, N
A. M>N
B. M<N
C. M=N
không tính kết quả,hãy so sánh:
M=1999*2001 và N=2000*2000
Dễ:
M=1999x(2000+1) N=2000x(1999+1)
M=1999x2000+1999x1 N=2000x1999+2000x1
Ta có:1999x1<2000x1
Cả M và N đều có chung 1999x2000
Suy ra M<N
Ta có M = 1999 x 2001 = 1999 x ( 2000 + 1)
suy ra M = 1999 x 2000 + 1999 (1)
Mặt khác : N = 2000 x 2000 = 2000 x ( 1999 + 1 )
suy ra : N = 2000 x 1999 + 2000 (2)
Từ ( 1) và (2) suy ra N > M
Từ (1) và (2) suy ra N >
Không tính kết quả cụ thể,hãy so sánh
M = 2012 x 2014 + 2016 và N = 2013 x 2013 + 2018
Hoạt động 3
Cho \(m = {2^7};\,n = {2^3}\)
a) Tính \({\log _2}\left( {mn} \right);{\log _2}m + {\log _2}n\) và so sánh các kết quả đó
b) Tính \({\log _2}\left( {\frac{m}{n}} \right);{\log _2}m - {\log _2}n\) và so sánh các kết quả đó
a: \(log_2\left(mn\right)=log_2\left(2^7\cdot2^3\right)=7+3=10\)
\(log_2m+log_2n=log_22^7+log_22^3=7+3=10\)
=>\(log_2\left(mn\right)=log_2m+log_2n\)
b: \(log_2\left(\dfrac{m}{n}\right)=log_2\left(\dfrac{2^7}{2^3}\right)=7-3=4\)
\(log_2m-log_2n=log_22^7-log_22^3=7-3=4\)
=>\(log_2\left(\dfrac{m}{n}\right)=log_2m-log_2n\)
a) \(\log_2\left(mn\right)=\log_2\left(2^7.2^3\right)=\log_22^{7+3}=\log_22^{10}=10.\log_22=10.1=10\)
\(\log_2m+\log_2n=\log_22^7+\log_22^3=7\log_22+3\log_22=7.1+3.1=7+3=10\)
b) \(\log_2\left(\dfrac{m}{n}\right)=\log_2\dfrac{2^7}{2^3}=\log_22^4=4.\log_22=4.1=4\)
\(\log_2m-\log_2n=\log_22^7-\log_22^3=7.\log_22-3\log_22=7.1-3.1=4\)
2. không tính kết quả, hay so sánh:
b) M= \(\dfrac{10^{2023}+1}{10^{2024}+1}\) và N= \(\dfrac{10^{2022}+1}{10^{2023}+1}\)
b) \(M=\dfrac{10^{2023}+1}{10^{2024}+1}< 1\) ( Vì tử < mẫu )
Ta có: \(M=\dfrac{10^{2023}+1}{10^{2024}+1}< \dfrac{10^{2023}+1+9}{10^{2024}+1+9}=\dfrac{10^{2023}+10}{10^{2024}+10}=\dfrac{10.\left(10^{2022}+1\right)}{10.\left(10^{2023}+1\right)}=\dfrac{10^{2022}+1}{10^{2023}+1}=N\)
Vì \(\dfrac{10^{2023}+1}{10^{2024}+1}< \dfrac{10^{2022}+1}{10^{2023}+1}\) nên \(M< N\)
bài 2 không tính kết quả hãy so sánh a và b
a) a=abc+pq+452
b=4bc+5q+ap2
b) a=mx(n+1)
b=nx(m+n)
c) a= 28x6x30
b= 29x6x29
trình bày nha
không tính kết quả hãy so sánh 2 biểu thức
M = 2121 x 232323
N = 2323 x 212121
a) Cho hai phân số: 1 n và 1 n + 1 (n ∈ Z, n > 0)
Hãy so sánh tích của hai phân số và hiệu của hai phân số trên.
b) Áp dụng kết quả trên để tính giá trị biểu thức sau:
M = 1 3.4 + 1 4.5 + 1 5.6 + 1 6.7 + 1 7.8 + 1 8.9 + 1 9.10 + 1 10.11
a)
1 n . 1 n + 1 = 1 n ( n + 1 ) 1 n − 1 n + 1 = n + 1 − n n ( n + 1 ) = 1 n ( n + 1 ) ⇒ 1 n . 1 n + 1 = 1 n − 1 n + 1
b) Áp dụng kết quả trên để tính giá trị biểu thức sau:
M = 1 3.4 + 1 4.5 + 1 5.6 + 1 6.7 + 1 7.8 + 1 8.9 + 1 9.10 + 1 10.11 M = 1 3 − 1 4 + 1 4 − 1 5 + 1 5 − 1 6 + 1 6 − 1 7 + 1 7 − 1 8 + 1 8 − 1 9 + 1 9 − 1 10 + 1 10 − 1 11 M = 1 3 − 1 11 M = 8 33