Chứng minh: B=

Những câu hỏi liên quan
A) cho a>b,b>0.Chứng minh a/b + b/a ≥2
B) cho a<b.Chứng minh; -2a - 3 > -2b - 3
C) chứng minh: x2 + 2y2 + 2xy + 6y +9 > 0
D) cho a + 3 > b + 3.Chứng minh: -5a + 1 < -5b +1
a: \(\dfrac{a}{b}+\dfrac{b}{a}>=2\cdot\sqrt{\dfrac{a}{b}\cdot\dfrac{b}{a}}=2\)
b: a<b
=>-2a>-2b
=>-2a-3>-2b-3
c: =x^2+2xy+y^2+y^2+6y+9
=(x+y)^2+(y+3)^2>=0 với mọi x,y
d: a+3>b+3
=>a>b
=>-5a<-5b
=>-5a+1<-5b+1
Đúng 1
Bình luận (0)
Cho hình vẽ bên: a) Chứng minh: tam giác OCB tam gíác ODE b) Chứng minh: góc B góc E c) Chứng minh: BC // DE C B O D E
Đọc tiếp
Cho hình vẽ bên: a) Chứng minh: tam giác OCB = tam gíác ODE
b) Chứng minh: góc B = góc E
c) Chứng minh: BC // DE ![]()
a: Xét ΔOCB và ΔODE có
OC=OD
CB=DE
OB=OE
Do đó: ΔOCB=ΔODE
Đúng 0
Bình luận (0)
Cho a>2, b>2.
a) Chứng minh a.b > a+b
b) Chứng minh a^2+b^2+c^2 ≥ ab+bc+ca
c) Chứng minh a^2+b^2+c^2+3 ≥ 2.(a+b+c)
d) Chứng minh a^2+b^2 ≥ 1/2 với a+b=1
e) Chứng minh a^2+b^2+c^2 ≥ 1/3 với a+b+c=1
Cho tỉ lệ thức: a/b: Chứng minh: a+b/b=c+d/d Chứng minh: a/a+b=c/c+d Chứng minh: 7a-5b/3a+2b= 7c-5d/3c+2d Chứng minh: ac/bd=(a+c/b+d)^2
mn ơi giúp mk với
a) chứng minh a song song với b
b) chứng minh c vuông góc với b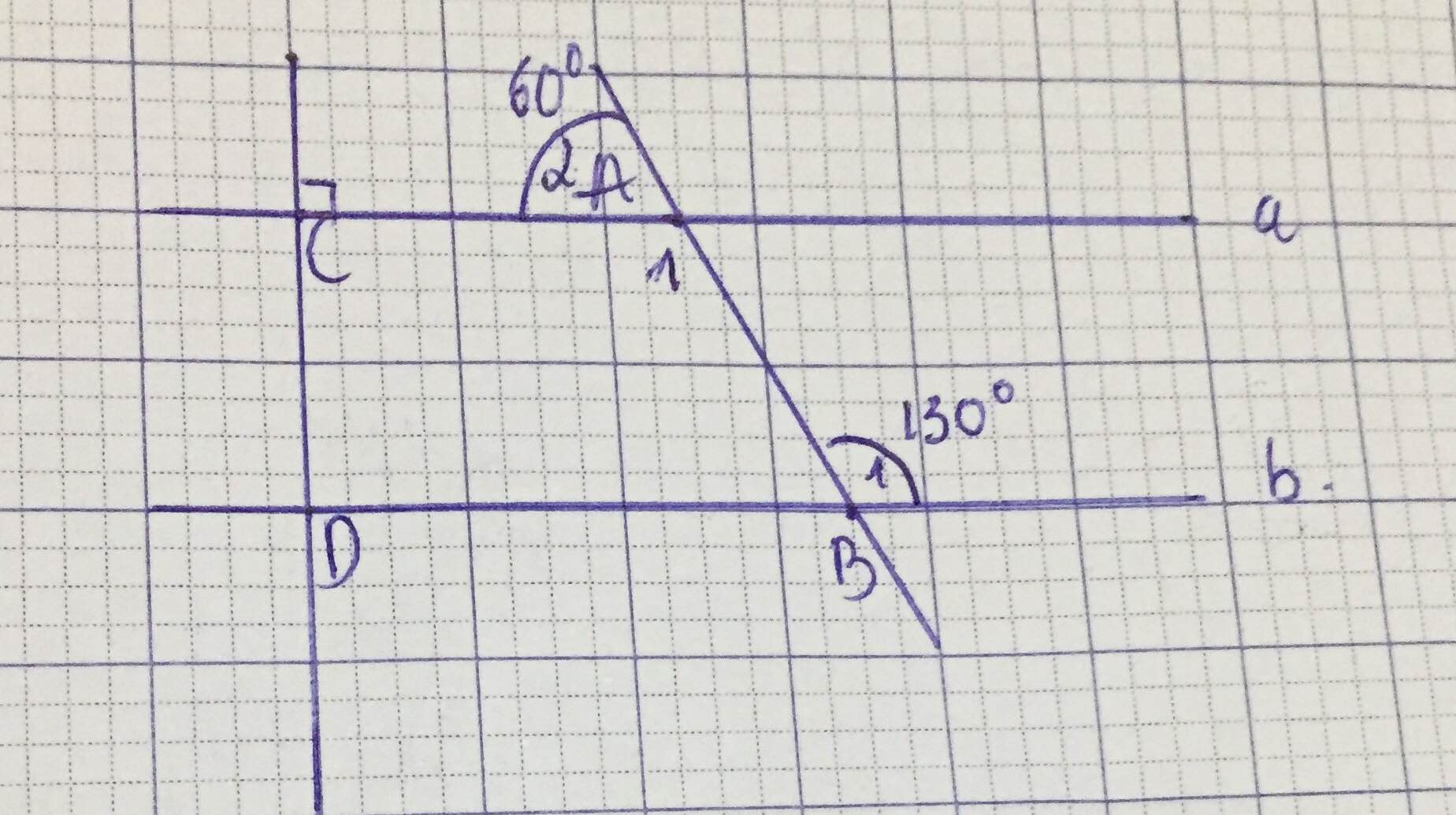
\(a,\) Muốn chứng minh \(a//b\) thì bạn phải sửa \(\widehat{B_1}=120\) nha
Ta có \(\widehat{A_1}+\widehat{A_2}=180\left(kề.bù\right)\Rightarrow\widehat{A_1}=180-\widehat{A_2}=120\)
Mà \(\widehat{B_1}=120\Rightarrow\widehat{A_1}=\widehat{B_1}\left(=120\right)\)
Mà 2 góc này ở vị trí so le trong
\(\Rightarrow a//b\)
\(b,\left\{{}\begin{matrix}a\perp c\left(GT\right)\\a//b\left(cmt\right)\end{matrix}\right.\Rightarrow b\perp c\)
Đúng 3
Bình luận (0)
Cho hình 3, biết A1B1= 100.a)Chứng minh a // b b)Chứng minh c⊥b
chứng minh a/b=c/d chứng minh a+b/b=c+d/d
Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow\hept{\begin{cases}a=kb\\c=kd\end{cases}}\)
\(\frac{a+b}{b}=\frac{kb+b}{b}=\frac{b\left(k+1\right)}{b}=k+1\)(1)
\(\frac{c+d}{d}=\frac{kd+d}{d}=\frac{d\left(k+1\right)}{d}=k+1\)(2)
Từ (1) và (2) => \(\frac{a+b}{b}=\frac{c+d}{d}\)=> đpcm
Ta có: \(\frac{a}{b}=\frac{c}{d}\)
\(\Leftrightarrow\frac{a}{b}+1=\frac{c}{d}+1\)
\(\Leftrightarrow\frac{a+b}{b}=\frac{c+d}{d}\)
\(\frac{a}{b}=\frac{c}{d}\)
\(\frac{a+b}{b}=\frac{c+d}{d}\Rightarrow min=\frac{1+2}{2}=\frac{2+4}{4}=\frac{3}{2}=\frac{6}{4}\)
\(\Leftrightarrow\frac{a+b}{b}=\frac{c+d}{d}\)
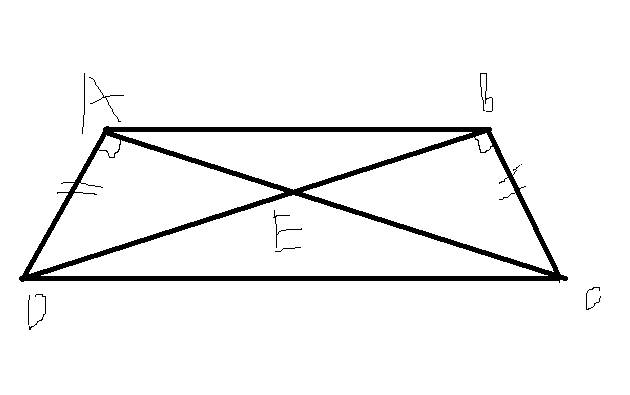
a) Chứng minh tam giác ADC = tam giác BCD
B) Chứng minh tam giác DEC cân
c) Chứng minh AB//CD
a: Xét ΔADC vuông tại A và ΔBCD vuông tại B có
AD=BC
DC chung
=>ΔADC=ΔBCD
b: ΔADC=ΔBCD
=>góc ACD=góc BDC
=>góc EDC=góc ECD
=>ΔEDC cân tại E
c: Xét ΔEAD vuông tại A và ΔEBC vuông tại B có
ED=EC
AD=BC
=>ΔEAD=ΔEBC
=>EA=EB
Xét ΔEAB và ΔECD có
EA/EC=EB/ED
góc AEB=góc CED
=>ΔEAB đồng dạng với ΔECD
=>góc EAB=góc ECD
=>AB//CD
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC, kẻ đường cao BE và CF cắt nhau tại H .a/ Chứng minh: b/ Chứng minh :AB.AF AE . ACc/ Chứng minh : AHBC.d/ Chứng minh . BH.BE+CH.CFBC2
Đọc tiếp
Cho tam giác nhọn ABC, kẻ đường cao BE và CF cắt nhau tại H ![]() .
.
a/ Chứng minh: ![]()
b/ Chứng minh :AB.AF = AE . AC
c/ Chứng minh : AH![]() BC.
BC.
d/ Chứng minh . BH.BE+CH.CF=BC2
b: Xét ΔABE vuông tại E và ΔACF vuông tại F có
góc BAE chung
=>ΔABE đồng dạng vớiΔACF
=>AB/AC=AE/AF
=>AB*AF=AC*AE
c: XétΔABC có
BE,CF là đường cao
BE cắt CF tại H
=>H là trực tâm
=>AH vuông góc BC
Đúng 0
Bình luận (0)
Cho hình chóp SABCD, đáy ABCD là hình vuông, SA vuông ABCD.
a) chứng minh rằng: CD vuông (SAD)
b) chứng minh: BC vuông (SAB)
c) chứng minh: AB vuông (SAD)
d) chứng minh: AD vuông (SAB)
e) chứng minh: BD vuông (SAC)
a: Ta có: CD\(\perp\)AD(ABCD là hình vuông)
CD\(\perp\)SA(SA\(\perp\)(ABCD))
AD,SA cùng thuộc mp(SAD)
Do đó: CD\(\perp\)(SAD)
b: Ta có: BC\(\perp\)AB(ABCD là hình vuông)
BC\(\perp\)SA(SA\(\perp\)(ABCD))
AB,SA cùng thuộc mp(SAB)
Do đó: BC\(\perp\)(SAB)
c: AB\(\perp\)AD(ABCD là hình vuông)
AB\(\perp\)SA(SA\(\perp\)(ABCD))
AD,SA cùng thuộc mp(SAD)
Do đó: AB\(\perp\)(SAD)
d: AD\(\perp\)AB
AD\(\perp\)SA(SA\(\perp\)(ABCD)))
SA,AB cùng thuộc mp(SAB)
Do đó: AD\(\perp\)(SAB)
e: BD\(\perp\)AC(ABCD là hình vuông)
BD\(\perp\)SA(SA\(\perp\)(ABCD))
AC,SA cùng thuộc mp(SAC)
Do đó: BD\(\perp\)(SAC)
Đúng 1
Bình luận (0)



















