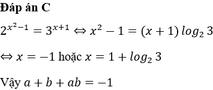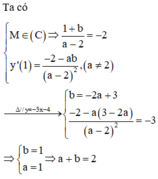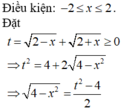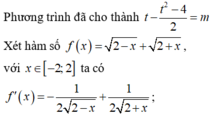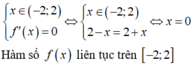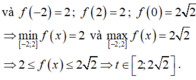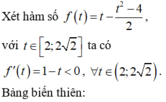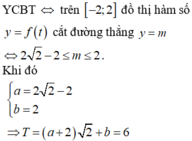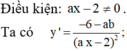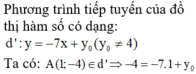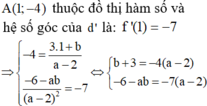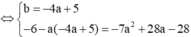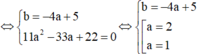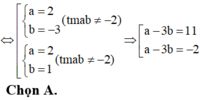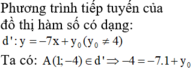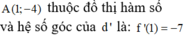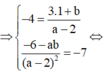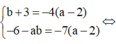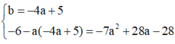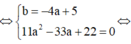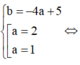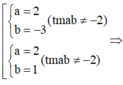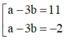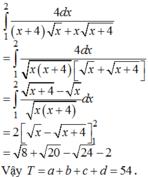Biết rằng: (66+a+b)x9-17=703
Khi đó, b+a-4 có giá trị bằng:

Những câu hỏi liên quan
Biết rằng phương trình
2
x
2
-
1
3
x
+
1
có 2 nghiệm là a, b. Khi đó a + b + ab có giá trị bằng A.
-
1
+
2
l
o
g
2
3
B.
1
+
l
o...
Đọc tiếp
Biết rằng phương trình 2 x 2 - 1 = 3 x + 1 có 2 nghiệm là a, b. Khi đó a + b + ab có giá trị bằng
A. - 1 + 2 l o g 2 3
B. 1 + l o g 2 3
C. -1
D. 1 + 2 l o g 2 3
Cho hàm số
y
x
+
b
a
x
−
2
có đồ thị là (C). Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của (C) tại điểm
M
1
;
−
2
song song với đường thẳng
3
x
+
y
−
4...
Đọc tiếp
Cho hàm số y = x + b a x − 2 có đồ thị là (C). Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của (C) tại điểm M 1 ; − 2 song song với đường thẳng 3 x + y − 4 = 0. Khi đó tổng giá trị của a + b bằng:
A. 2
B. 1
C. -1
D. 0
Biết rằng phương trình
2
-
x
+
2
+
x
-
4
-
x
2
m
có nghiệm khi m thuộc [a;b] với a,b
∈
ℝ
. Khi đó giá trị của
T...
Đọc tiếp
Biết rằng phương trình 2 - x + 2 + x - 4 - x 2 = m có nghiệm khi m thuộc [a;b] với a,b ∈ ℝ . Khi đó giá trị của T = ( a + 2 ) 2 + b là?
A. T = 3 2 + 2
B. T = 6
C. T = 8
D. T = 0
Biết rằng phương trình
2
−
x
+
2
+
x
−
4
−
x
2
m
có nghiệm khi m thuộc [a;b] với
a
,
b
∈
ℝ
. Khi đó giá trị của biểu thức
T
a
+
2...
Đọc tiếp
Biết rằng phương trình 2 − x + 2 + x − 4 − x 2 = m có nghiệm khi m thuộc [a;b] với a , b ∈ ℝ . Khi đó giá trị của biểu thức T = a + 2 2 + b là
A. T = 3 2 + 2
B. T = 6
C. T = 8
D. T = 0
Đáp án B
Đặt t = 2 − x + 2 + x ⇔ t 2 = 4 + 2 4 − x 2 ⇔ 4 − x 2 = t 2 − 4 2 và x ∈ − 2 ; 2 ⇒ t ∈ 2 ; 2 2
Khi đó, phương trình đã cho trở thành: t − t 2 − 4 2 = m ⇔ 2 m = − t 2 + 2 t + 4 = f t .
Xét hàm số f t = − t 2 + 3 t + 4 trên đoạn 2 ; 2 2 ⇒ min 2 ; 2 2 f t = − 4 + 4 2 ; m a x 2 ; 2 2 f t = 4
Do đó, để phương trình f t = 2 m có nghiệm ⇔ − 2 + 2 2 ≤ m ≤ 2 ⇒ a = − 2 + 2 2 b = 2
Vậy T = a + 2 2 + b − 2 + 2 2 + 2 2 + 2 = 6
Đúng 0
Bình luận (0)
Biết rằng : | a+7 |+| b-3 |=0. Khi đó tổng a + b có giá trị là
theo bài ra ta có: | a+7 | + | b-3 | = 0
=> a+7=0 và b-3 = 0
với a+7 =0 => a= 0-7 = -7
với b-3 = 0 => b= 3+0 =3
vậy a+b = -7 + 3 = -4
vậy a+b có giá trị bằng -4
Đúng 0
Bình luận (0)
Cho hàm số y
3
x
+
b
ax
-
2
(
ab
≠
-
2
)
. Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của đồ thị hàm số tại điểm A(1;-4) song song với đường thẳng d: 7x + y -40. Khi đó giá trị của a-3b bằng:...
Đọc tiếp
Cho hàm số y= 3 x + b ax - 2 ( ab ≠ - 2 ) . Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của đồ thị hàm số tại điểm A(1;-4) song song với đường thẳng d: 7x + y -4=0. Khi đó giá trị của a-3b bằng:
A. -2
B. 4
C. 5
D. -1
Cho hàm số y
3
x
+
b
a
x
-
2
(
a
b
≠
-
2
)
. Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của đồ thị hàm số tại điểm A(1;-4) song song với đường thẳng d: 7x+y-40. Khi đó giá trị của a-3b bằng: A. -2 B. 4 C. 5 D. -1
Đọc tiếp
Cho hàm số y = 3 x + b a x - 2 ( a b ≠ - 2 ) . Biết rằng a và b là các giá trị thỏa mãn tiếp tuyến của đồ thị hàm số tại điểm A(1;-4) song song với đường thẳng d: 7x+y-4=0. Khi đó giá trị của a-3b bằng:
A. -2
B. 4
C. 5
D. -1
Biết rằng
∫
1
2
4
d
x
x
+
4
x
+
x
x
+
4
a
+
b
-
c...
Đọc tiếp
Biết rằng ∫ 1 2 4 d x x + 4 x + x x + 4 = a + b - c - d . Lúc đó giá trị T=a + b + c +d bằng:
A. 52
B. 48
C. 46
D. 54
biết rằng phương trình \(x^2+px+1=0\) có nghiệm là a,b và phương trình \(x^2+qx+2=0\) có nghiêm là b,c . Khi đó giá trị của biểu thức \(A=pq-\left(b-a\right)\left(b-c\right)\)bằng ?
Áp dụng viet vào pt \(x^2+px+1=0\) ta được:\(\left\{{}\begin{matrix}a+b=-p\\ab=1\end{matrix}\right.\)
Áp dụng viet vào pt \(x^2+qx+2=0\) ta được:\(\left\{{}\begin{matrix}b+c=-q\\bc=2\end{matrix}\right.\)
\(A=pq-\left(b-a\right)\left(b-c\right)=-\left(a+b\right).-\left(b+c\right)-\left(b^2-bc-ab+ac\right)\)
\(=ab+ac+b^2+bc-b^2+bc+ab-ac\)
\(=2ab+2bc=6\)
Đúng 3
Bình luận (0)
Phương trình: \(x^2+px+1=0\)
Có 2 nghiệm:a,b
\(\Rightarrow\left\{{}\begin{matrix}a+b=-p\\a.b=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}p=-\left(a+b\right)\\1=a.b\end{matrix}\right.\)
Phương trình \(x^2+px+2=0\)
Có 2 nghiệm:b,c
\(\Rightarrow\left\{{}\begin{matrix}b+c=-q\\b.c=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}q=-\left(b+c\right)\\2=b.c\end{matrix}\right.\)
Ta có: \(p.q-\left(b-a\right)\left(b-c\right)\)
\(=-\left(a+b\right).\left[-\left(b+c\right)\right]-\left(b-a\right)\left(b-c\right)\)
\(=\left(a+b\right)\left(b+c\right)-\left(b-a\right)\left(b-c\right)\)
\(=ab+ac+b^2+bc-b^2+bc+ab-ac\)
=\(\left(ab+ab\right)+\left(ac-ac\right)+\left(b^2-b^2\right)+\left(bc+bc\right)\)
\(=2ab+2bc\)
\(=2.1+2.2\)
=6
-Chúc bạn học tốt-
Đúng 1
Bình luận (0)