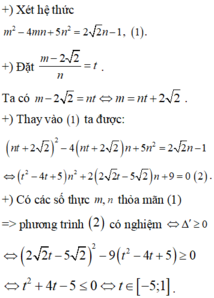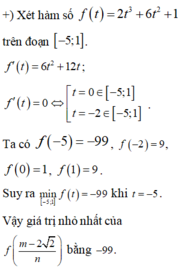Tìm số tự nhiên n thỏa mãn 20 + 21 + 22 +...+ 221 = 22n - 1

Những câu hỏi liên quan
Câu 9
Số tự nhiên nn thỏa mãn 2^0+2^1+2^2+...+2^{21}=2^{2n}-120+21+22+...+221=22n−1 là n=n=
Tìm tất cả các số tự nhiên n để p=1+2+22+...+22n-1 là số nguyên tố
\(p=1+2+2^2+\cdots+2^{2n-1}\)
=>\(2p=2+2^2+2^3+\cdots+2^{2n}\)
=>\(2p-p=2+2^2+2^3+\cdots+2^{2n}-1-2-2^2-\cdots-2^{2n-1}\)
=>\(p=2^{2n}-1=4^{n}-1\)
TH1: n=0
=>\(p=4^0-1=1-1=0\) (loại)
TH2: n=1
\(p=4^1-1=4-1=3\) là số nguyên tố
=>Nhận
TH3: n>1
=>\(p=4^{n}-1=\left(4-1\right)\left(4^{n-1}+4^{n-2}+\cdots+1\right)\)
=>p là tích của hai số tự nhiên lớn hơn 1
=>p là hợp số
=>Loại
Vậy: n=1
Đúng 0
Bình luận (0)
các bn giúp mình giải 1 số bài tập này nhé :
-tìm số tự nhiên n thỏa mãn :n+3 chia hết cho n-2
-tìm số tự nhiên n thỏa mãn :n+3 chia hết cho 2n -2
-tìm các số nguyên x thỏa mãn x lớn hơn hoặc bằng -21/7 và x bé hơn hoặc bằng 3
-tìm các số tự nhiên x,y thỏa mãn x-1 chia hết cho y , y-1 chia hết cho x
Tìm số hữu tỉ x thỏa mãn: \(\dfrac{x+4}{20}+\dfrac{x+3}{21}=\dfrac{x+2}{22}+\dfrac{x+1}{21}\)
Tìm các số tự nhiên n thỏa mãn mỗi bất phương trình sau: n + 2 2 – (n – 3)(n + 3) ≤ 40
Ta có: n + 2 2 – (n – 3)(n + 3) ≤ 40
⇔ n 2 + 4n + 4 – n 2 + 9 ≤ 40
⇔ 4n < 40 – 13
⇔ n < 27/4
Vậy các số tự nhiên cần tìm là 0; 1; 2; 3; 4; 5; 6.
Đúng 0
Bình luận (0)
Câu 15. Tìm số tự nhiên m thỏa mãn 202018 20m 202020?A. m 2020. B. m 2019. C. m 2018. D. m 20.Câu 16. Tìm số tự nhiên n thỏa mãn 3n 81A. n 2 B. n 3 C. n 4 D. n 8Câu 17: Viết kết quả phép tính sau dưới dạng một luỹ thừa: 87: 8 là:A. 86 B. 85 C. 84 D. 83Câu 18: Cho biều thức M 75 + 120 + x. Giá trị nào của x dưới đây thì M...
Đọc tiếp
Câu 15. Tìm số tự nhiên m thỏa mãn 202018 < 20m < 202020?
A. m = 2020. B. m = 2019. C. m = 2018. D. m = 20.
Câu 16. Tìm số tự nhiên n thỏa mãn 3n = 81
A. n = 2 B. n = 3 C. n = 4 D. n = 8
Câu 17: Viết kết quả phép tính sau dưới dạng một luỹ thừa: 87: 8 là:
A. 86 B. 85 C. 84 D. 83
Câu 18: Cho biều thức M = 75 + 120 + x. Giá trị nào của x dưới đây thì M ⋮ 3
A.x = 7 B.x= 5 C.x =4 D.x =12
Câu 19: Tổng nào sau đây chia hết cho 7 ?
A.49 + 70 B.14 + 51 C.7 + 134 D.10+16
Câu 20: Số tự nhiên m chia cho 45 dư 20 có dạng là:
A. 45 + 20k B. 45k – 20 C. 45 – 20k D. 45k + 20
Câu 21: Điền chữ số vào dấu * để chia hết cho 3:
A. {0; 3; 6}. B.{1; 3; 6; 9}. C.{3; 6; 9}. D.{0; 6; 9}.
15.B
16.C
17.A
18.D
19.A
còn câu 20,21 mình sợ mình làm sai nên k ghi đáp án sorry bạn nha:(
Đúng 0
Bình luận (0)
a, tìm số tự nhiên n sao cho 18 - 5n chia hết cho n - 1
b, tìm cặp số tự nhiên x; y thỏa mãn: ( x + 3 ).( 2y - 1 ) = 20
Tìm số tự nhiên n để 22n+2n+1\(⋮\)7
Lời giải:
Với $k\in\mathbb{N}$.
Nếu $n=3k$ thì:
$2^{2n}+2^n+1=2^{6k}+2^{3k}+1=64^k+8^k+1$
$\equiv 1^k+1^k+1\equiv 3\pmod 7$ (loại)
Nếu $n=3k+1$ thì:
$2^{2n}+2^n+1=2^{6k+2}+2^{3k+1}+1$
$=4.64^k+2.8^k+1\equiv 4+2+1\equiv 7\equiv 0\pmod 7$
Nếu $n=3k+2$ thì:
$2^{2n}+2^n+1=2^{6k+4}+2^{3k+2}+1$
$=16.64^k+4.8^k+1\equiv 16+4+1\equiv 0\pmod 7$
Vậy chỉ cần $n$ không chia hết cho $3$ thì $2^{2n}+2^n+1\vdots 7$
Đúng 1
Bình luận (0)
Tìm các số tự nhiên n thỏa mãn 20:(2n+3)
Ta có: 20 chia hết cho (2n+3) và n là số tự nhiên
=> (2n+3) thuộc Ư(20)={1;2;4;5;10;20}
Nếu 2n + 3 = 1 => n = 4
Nếu 2n + 3 = 2 => n = 5/2 (loại)
Nếu 2n + 3 = 4 => n = 1/2 (loại)
Nếu 2n + 3 = 5 => n = 4
Nếu 2n + 3 = 10 => n = 7/2 9loaị)
Nếu 2n + 3 = 20 => n = 17/2 (loại)
Vậy ta tìm được giá trị của n là 4
CHÚC BẠN HỌC TỐT
Đúng 0
Bình luận (0)
Cho hàm số
f
(
x
)
2
x
3
+
6
x
2
+
1
và các số thực m,n thỏa mãn
m
2
-
4
m
n
+
5
n
2
...
Đọc tiếp
Cho hàm số f ( x ) = 2 x 3 + 6 x 2 + 1 và các số thực m,n thỏa mãn m 2 - 4 m n + 5 n 2 = 2 2 n - 1 . Giá trị nhỏ nhất của f m - 2 2 n bằng
A. -99 .
B. -100.
C. 5.
D. 4.