

Giải 3 bài đó giúp mik với
Ai đó giúp mik giải bài này với
3. A (trọng âm rơi vào âm 2, A và C âm 1 - D mờ quá em à)
4. B (trọng âm rơi vào âm 3, A và C âm 2 - D thì không nhìn rõ được là từ gì)
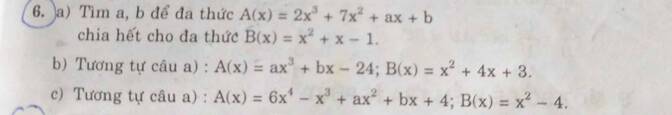
ai đó giải giúp mik bài này với ạ
a, ta có A(x)=2x3+7x2+ax+b
=(2x3+2x2+2x)+(5x2+5x+5)+ax-7x+b-5
=2x(x2+x+1)+5(x2+x+1)+(a-7)x+(b-5)
=(x2+x+1)(2x+5)+(a-7)x+(b-5)
ta có: (x2+x+1)(2x+5)⋮B(x)
→để A(x)⋮B(x) thì (a-7)x+(b-5)=0
→\(\left\{{}\begin{matrix}a-7=0\\b-5=0\end{matrix}\right.\) ⇔\(\left\{{}\begin{matrix}a=7\\b=5\end{matrix}\right.\)
vậy ....
mk trình bày hơi tắt xíu
bn cố gắng dịch nhé
a) \(A\left(x\right)=2x^3+7x^2+ax+b=\left(x^2+x-1\right)\left(2x+5\right)+\left(a-3\right)x+b+5\)
\(=\left(2x+5\right)B\left(x\right)+\left(a-3\right)x+b+5\)
Để \(A\left(x\right)\) chia hết cho \(B\left(x\right)\) thì
\(\left(a-3\right)x+b+5=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a-3=0\\b+5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=3\\b=-5\end{matrix}\right.\)
b) \(A\left(x\right)=ax^3+bx-24=\left(ax-4a\right)\left(x^2+4x+3\right)+\left(b+13a\right)x+12a-24\)
\(=\left(ax-4a\right)\left(x^2+4x+3\right)+\left(b+13a\right)x+12a-24\)
Để \(A\left(x\right)\) chia hết cho \(B\left(x\right)\) thì
\(\left(b+13a\right)x+12a-24=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}b+13a=0\\12a-24=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=-26\end{matrix}\right.\)
c) Tương tự.

mn ơi giúp mik giải mấy bài đó đc hog :< mik bí quá à :< camon mn trc vì đã help mik :3
1:
#include <bits/stdc++.h>
using namespace std;
long long t,i,n;
int main()
{
cin>>n;
t=0;
for (i=1; i<=n; i++) t+=i;
cout<<t;
return 0;
}
Bài 2:
#include <bits/stdc++.h>
using namespace std;
long long n,i,t;
int main()
{
cin>>n;
t=0;
for (i=1; i<=n; i++)
if (i%2==0) t+=i;
cout<<t;
return 0;
}
Bài 3:
#include <bits/stdc++.h>
using namespace std;
long long n,i,t;
int main()
{
cin>>n;
t=0;
for (i=1; i<=n; i++)
if (i%2!=0) t+=i;
cout<<t;
return 0;
}
Bài 4:
#include <bits/stdc++.h>
using namespace std;
long long n,i,t;
int main()
{
cin>>n;
t=0;
for (i=1; i<=n; i++)
if (i%3==0) t+=i;
cout<<t;
return 0;
}
Bài 5:
#include <bits/stdc++.h>
using namespace std;
long long n,i,t;
int main()
{
cin>>n;
t=1;
for (i=1; i<=n; i++)
t*=i;
cout<<t;
return 0;
}
Giúp mik với đi mà . Giải cho mik B5 nha . Hoặc giải chi mik 2 bài nha. Giải rõ ràng giúp mik với ạ . Giúp với 
 giải chi tiết giúp mik bài 3 với mik đang cần gấp
giải chi tiết giúp mik bài 3 với mik đang cần gấp
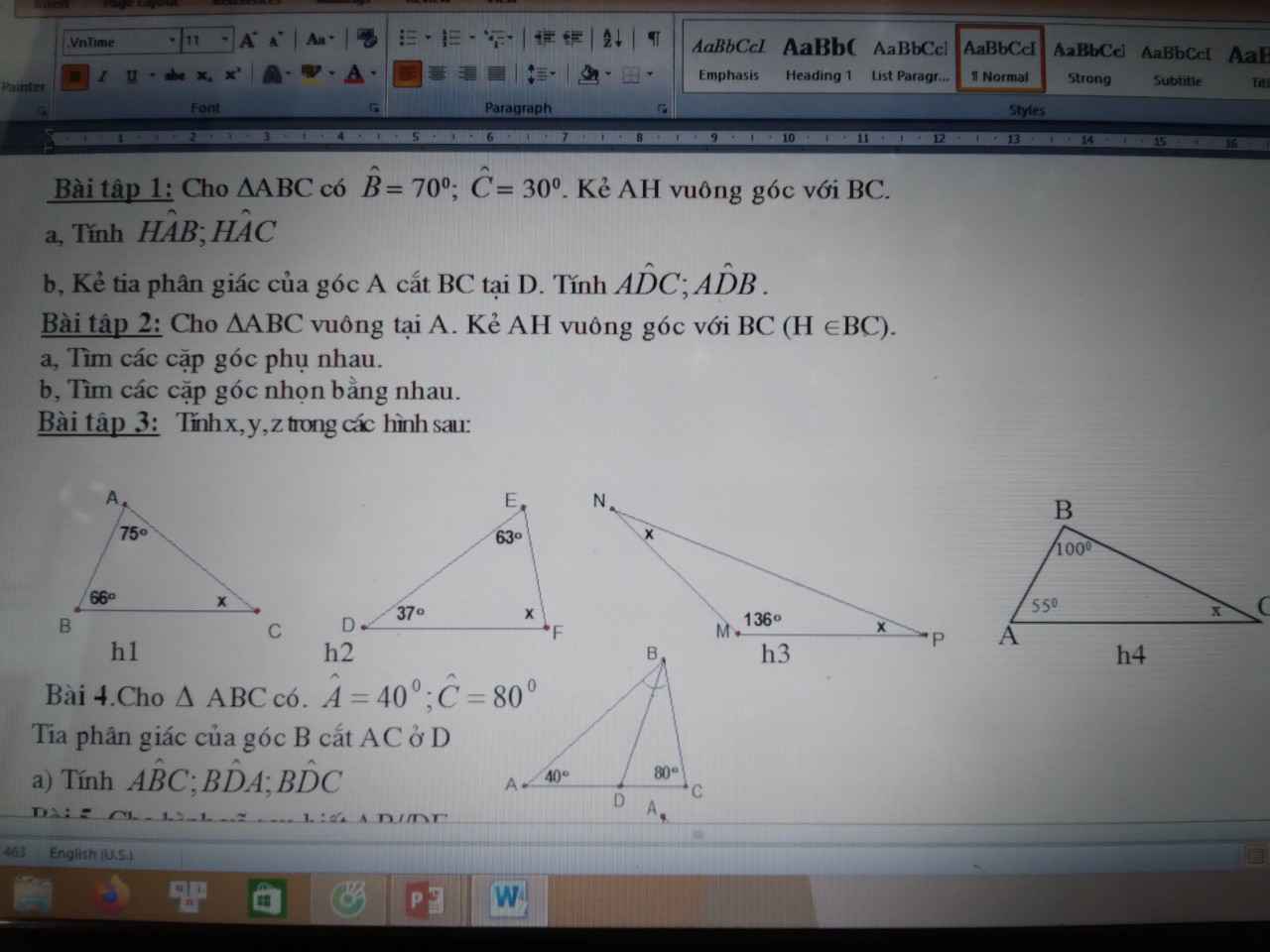
h1) Ta có : ^A + ^B + ^C = 1800
=> 750 + 660 + x = 1800
<=> x = 1800 - 750 - 660 = 390
h2) Ta có : ^E + ^D + ^F = 1800
=> 630 + 370 + x = 1800
<=> x = 1800 - 1000 = 800
h3) Ta có : ^N + ^M + ^P = 1800
=> 1360 + x + x = 1800 <=> 2x = 440 <=> x = 220
=> ^N = ^P = x = 220
h4) Ta có : ^A + ^B + ^C = 1800
=> 1000 + 550 + x = 1800
<=> x = 1800 - 1000 - 550 = 250
BÀI 7: Một hình thoi có tổng độ dài hai đường chéo là 104cm. Đường chéo dài gấp 3 lần đường chéo ngắn . Tính diện tích hình thoi đó .
giúp mik với. Bài cúi mik hỏi ( phần Toán ) hôm nay nha. giải rõ ràng nhé
Tổng số phần bằng nhau là :
3 + 1 = 4 ( phần )
Đường chéo ngắn là :
104 : 4 x 1 = 26 ( cm )
Đường chéo dài là :
104 - 26 = 78 ( cm )
Vậy diện tích hình thoi là \(\dfrac{26\times78}{2}=1014(cm2)\)
ta có sơ đồ:
đường chéo dài :l---l---l---l 104 cm
đường chéo ngắn :l---l
Tổng số phần bằng nhau là :
3 + 1 = 4 ( phần )
Đường chéo ngắn là :
104 : 4 x 3 = 78 ( cm )
Đường chéo dài là :
104 - 78= 26( cm )
Vậy diện tích hình thoi là
78 x 26 : =1014 ( cm2)
Đường chéo dài là:
104:(3+1)x3=78(cm)
Đường chéo ngắn là:
104-78=26(cm)
Diện tích hình thoi lầ:
78x26:2=1014(cm)
đ/s:.
giải giúp mik bài 3 với ạ !!!
b: Xét tứ giác ABCK có
M là trung điểm của AC
M là trung điểm của BK
Do đó: ABCK là hình bình hành
Suy ra: BC=AK

giải giúp mik bài 3 với ạ
\(53,\sqrt{\left(a-2b\right)^2}\left(a\le2b\right)\)
\(=\left|a-2b\right|=-a+2b\)
\(54,\sqrt{4x^2-4xy+y^2}\left(2x\ge y\right)\)
\(=\sqrt{\left(2x-y\right)^2}=\left|2x-y\right|=2x-y\)
\(55,\sqrt{\left(2x-1\right)^2}\left(x\ge\dfrac{1}{2}\right)\)
\(=\left|2x-1\right|=2x-1\)
\(56,\sqrt{\left(3a-2\right)^2}\left(3a\le2\right)\)
\(=\left|3a-2\right|=-3a+2\)
\(57,\sqrt{\left(6-9x\right)^2}\left(3x\ge2\right)\)
\(=\left|6-9x\right|=-6+9x\)
\(58,\sqrt{25a^2-10a+1}\left(5a\le1\right)\)
\(=\sqrt{\left(5a-1\right)^2}=\left|5a-1\right|=-5a+1\)
\(59,\sqrt{m^2+4mn+4n^2}\left(m\ge-2n\right)\)
\(=\sqrt{\left(m+2n\right)^2}=\left|m+2n\right|=m+2n\)
\(60,\sqrt{9x^2-24xy+16y^2}\left(3x\le4y\right)\)
\(=\sqrt{\left(3x-4y\right)^2}=\left|3x-4y\right|=-3x+4y\)
Bài 3:
53. \(\sqrt{\left(a-2b\right)^2}=\left|a-2b\right|=2b-a\)
54. \(\sqrt{4x^2-4xy+y^2}=\sqrt{\left(2x-y\right)^2}=\left|2x-y\right|=2x-y\)
55. \(\sqrt{\left(2x-1\right)^2}=\left|2x-1\right|=2x-1\)
56. \(\sqrt{\left(3a-2\right)^2}=\left|3a-2\right|=2-3a\)
57. \(\sqrt{\left(6-9x\right)^2}=\left|6-9x\right|=6-9x\)
58. \(\sqrt{25a^2-10a+1}=\sqrt{\left(5a-1\right)^2}=\left|5a-1\right|=1-5a\)
59. \(\sqrt{m^2+4mn+4n^2}=\sqrt{\left(m+2n\right)^2}=\left|m+2n\right|=m+2n\)
60. \(\sqrt{9x^2-24xy+16y^2}=\sqrt{\left(3x-4y\right)^2}=\left|3x-4y\right|=4y-3x\)
giải giúp mik bài 3 với cảm ơn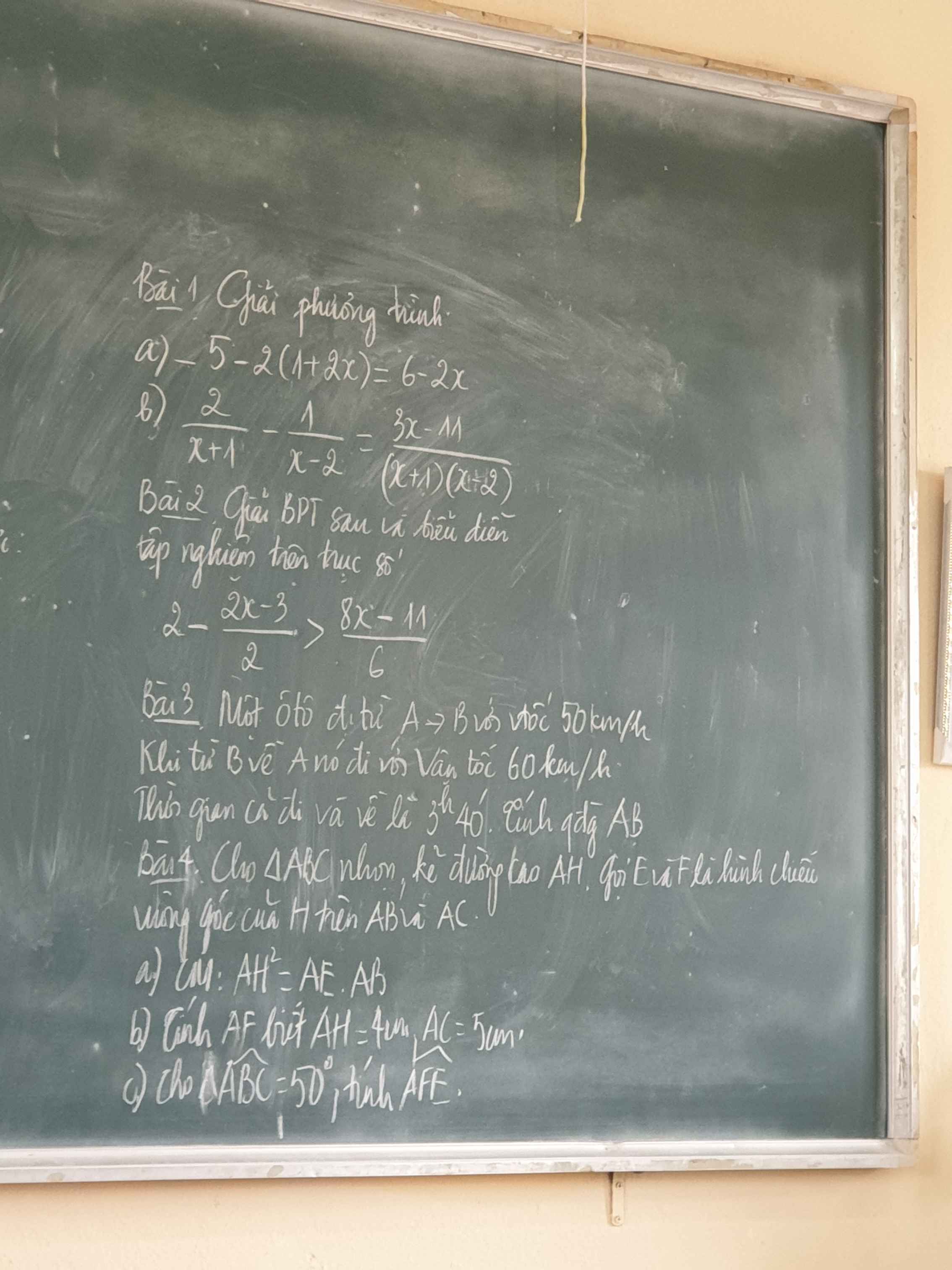
3h40p= \(\dfrac{11}{3}\) giờ
gọi thời gian đi là: x
thời gian về là: \(\dfrac{11}{3}\)-x
theo đề ta có:
50x=60(\(\dfrac{11}{3}\)-x)
<=> 50x= 220-60x
<=>50x+60x=220
<=>110x=220
<=>x=2
Quãng đường từ A -> B là:
50.2=100 (km)