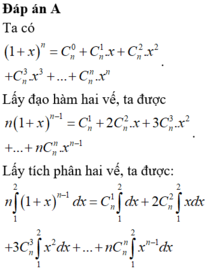\(2^2\cdot3^{2n}\cdot\left(\frac{2}{3}\right)^n\cdot2^n=82944\)

\(2^2\cdot\left(3^2\right)^n\cdot\left(\frac{2^n}{3^n}\right)\cdot2^n=82944\)

\(2^2\cdot9^n\cdot\frac{2^n}{3^n}\cdot2^n=82944\)

\(2^2\cdot\frac{9^n\cdot2^n}{3^n}\cdot2^n=82944\)

\(2^2\cdot\frac{18^n}{3^n}\cdot2^n=82944\)

\(4\cdot6^n\cdot2^n=82944\)

\(6^n\cdot2^n=82944:4\)

\(12^n=20736\)

\(12^n=12^4\)

Vậy n=4

Ta có

1 + x n = C n 0 + C n 1 x + C n 2 x 2 + C n 3 x 3 + . . . + C n n x n

Lấy đạo hàm hai vế, ta được

n 1 + x n - 1 = C n 1 + 2 C n 2 x + 3 C n 3 x 2 + . . . + n C n n x n - 1

Lấy tích phân hai vế, ta được:

n ∫ 1 2 1 + x n - 1 d x = C n 1 ∫ 1 2 d x + 2 C n 2 ∫ 1 2 x d x + 3 C n 3 ∫ 1 2 x 2 d x + . . . + n C n n ∫ 1 2 x n - 1 d x

Tính toán các tích phân trên, ta được:

C n 1 + 3 C n 2 + 7 C n 3 + . . . + 2 n - 1 C n n = 3 n - 2 n

Theo đề ta có: 

3 n - 2 n = 3 2 n - 2 n - 6480 ⇔ 3 2 n - 3 n - 6480 = 0

Giải phương trình mũ này ta tìm được n = 4. Vậy n = 4 là nghiệm của phương trình đã cho

Đáp án A

a) S hình thoi là:

      (19 x 12) : 2 = 114(cm2)

b) S hình thoi là;

      (30 x 7) : 2 = 105(cm2)

\(2^n.3^{2n}.\left(\frac{2}{3}\right)^n.2^n=82944\)(n\(\in\)N)

\(2^n.2^n.\left(\frac{2}{3}\right)^n.\left(3^2\right)^n=82944\)

\(\left(2.2.\frac{2}{3}.9\right)^n=82944\)

\(24^n=82944\)

Tớ làm đến đây thôi khó lắm bạn xem lại đề đi

\(2^2.3^{2n}.\left(\frac{2}{3}\right)^n.2^n=82944\)

\(2^2.9^n.\left(\frac{2}{3}\right)^n.2^n=2^{10}.3^4\)

\(2^2.2^n.\left(\frac{2}{3}.9\right)^n=2^{10}.3^4\)

\(2^{n+2}.6^n=2^{10}.3^4\)

\(2^{n+2}.2^n.3^n=2^{10}.3^4\)

\(2^{2n+2}.3^n=2^{10}.3^4\)

Vậy n = 4