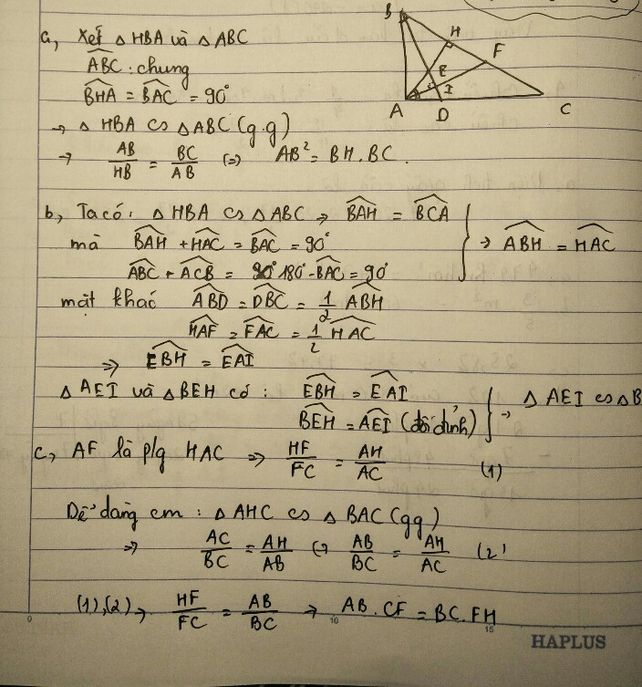Cho tam giác ABC vuông tại góc A có B=2C, AB=3cm. Vẽ đường cao AH (H thuộc AB)
a)CM: tam giác HBA đồng dạng với tam giác ABC
b)Kẻ tia phân giác của góc ABC cắt AH tại D cắt AC tại E. CM:AB2=AE.AC
c)CM: tam giác BHD đồng dạng với tam giác BAE rồi suy ra tỉ số diện tích hai tam giác BHD và BAE