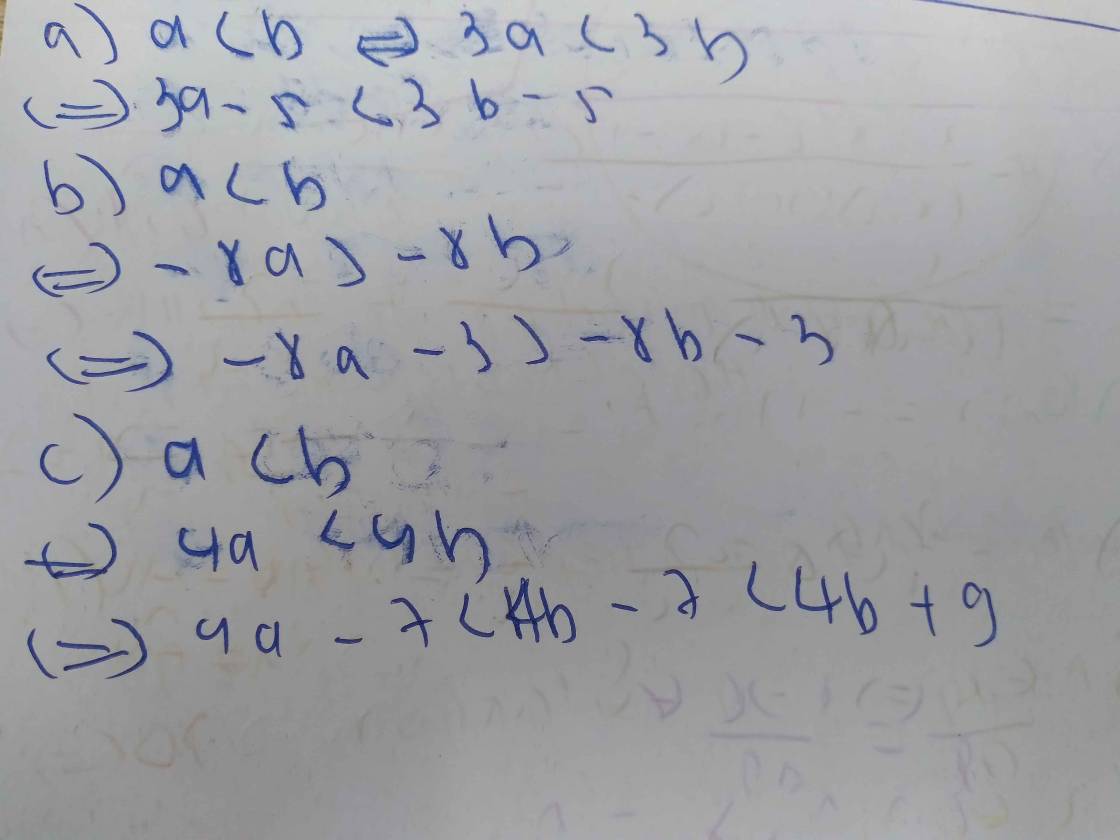`Answer:`

a. Ta có: \(\frac{a}{b}=\frac{1}{3}\Rightarrow\frac{a}{1}=\frac{b}{3}\)

Đặt \(k=\frac{a}{1}=\frac{b}{3}\Rightarrow\hept{\begin{cases}a=k\\b=3k\end{cases}}\)

\(E=\frac{3a+2b}{4a-3b}\)

\(=\frac{3k+2.3k}{4k-3.3k}\)

\(=\frac{3k+6k}{4k-9k}\)

\(=\frac{9k}{-5k}\)

\(=-\frac{9}{5}\)

b. Thay `a-b=5` vào biểu thức `F`, ta được:

\(F=\frac{3a-\left(a-b\right)}{2a+b}-\frac{4b+\left(a-b\right)}{a+3b}\)

\(=\frac{3a-a+b}{2a+b}-\frac{4b+a-b}{a+3b}\)

\(=\frac{2a+b}{2a+b}-\frac{3b+a}{a+3b}\)

\(=1+1\)

\(=0\)

a) \(G=\frac{\frac{3a}{b}-\frac{2b}{b}}{\frac{a}{b}-\frac{3b}{b}}=\frac{3.\frac{10}{3}-2}{\frac{10}{3}-3}=\frac{10-2}{\frac{1}{3}}=24\)

b) \(H_1=\frac{\frac{2a-3b}{b}}{\frac{4a+3b}{b}}=\frac{\frac{2a}{b}-\frac{3b}{b}}{\frac{4a}{b}+\frac{3b}{b}}=\frac{2.\frac{10}{3}-3}{4.\frac{10}{3}+3}=\frac{\frac{11}{3}}{\frac{49}{3}}=\frac{11}{49}\)

\(H_2=\frac{\frac{5a-4b}{b}}{\frac{3a+b}{b}}=\frac{5.\frac{a}{b}-4}{3.\frac{a}{b}+1}=\frac{5.\frac{10}{3}-4}{3.\frac{10}{3}+1}=\frac{\frac{38}{3}}{\frac{33}{3}}=\frac{38}{33}\)

=> \(H=\frac{11}{49}-\frac{38}{33}=\frac{-1499}{1617}\)

\(\dfrac{a}{b}=\dfrac{1}{3}\)

nên b=3a

\(E=\dfrac{3a+2b}{4a-3b}=\dfrac{3a+6a}{4a-9a}=\dfrac{9}{-5}=-\dfrac{9}{5}\)

a-b=5 nên a=b+5

\(F=\dfrac{3\left(b+5\right)-5}{2\left(b+5\right)+b}-\dfrac{4b+5}{b+5+3b}\)

\(=\dfrac{3b+10}{3b+10}-1=1-1=0\)

a)

`a<b`

`<=>3a<3b`

`<=>3a-5<3b-5`

b)

`a<b`

`<=>-8a> -8b`

`<=>-8a-3> -8b-3`

c)

`a<b`

`<=>4a<4b`

`<=>4a+9<4b+9`

mà `4a-7<4a+9`

`<=>4a-7<4b+9`

4a-b=6 nên b=4a-6

\(\dfrac{6a-b}{3a+5}-\dfrac{4a-4b}{3b-5}\)

\(=\dfrac{6a-\left(4a-6\right)}{3a+5}-\dfrac{4a-4\left(4a-6\right)}{3\left(4a-6\right)-5}\)

\(=\dfrac{6a-4a+6}{3a+5}-\dfrac{4a-16a+24}{12a-18-5}\)

\(=\dfrac{2a+6}{3a+5}-\dfrac{-12a+24}{12a-23}\)

\(=\dfrac{2a+6}{3a+5}+\dfrac{12a-24}{12a-23}\)

\(=\dfrac{\left(2a+6\right)\left(12a-23\right)+\left(12a-24\right)\left(3a+5\right)}{\left(3a+5\right)\left(12a-23\right)}\)

\(=\dfrac{24a^2-46a+72a-138+36a^2+60a-72a-120}{\left(3a+5\right)\left(12a-23\right)}\)

\(=\dfrac{60a^2+14a-258}{\left(3a+5\right)\left(12a-23\right)}\)

Câu 5:

\(D\left(2\right)=21a+9b-6a-4b\)

\(D\left(2\right)=\left(21a-6a\right)+\left(9b-4b\right)\)

\(D\left(2\right)=15a+5b\)

Mà: \(3a+b=18\Rightarrow b=18-3b\)

\(\Rightarrow D\left(2\right)=15a+5\left(18-3b\right)\)

\(D\left(2\right)=15a+90-15a\)

\(D\left(2\right)=90\)

Vậy: ...

Câu 4:

\(D\left(1\right)=4a+10b-b+2a\)

\(D\left(1\right)=\left(4a+2a\right)+\left(10b-b\right)\)

\(D\left(1\right)=6a+9b\)

Mà: \(2a+3b=12\Rightarrow a=\dfrac{12-3b}{2}\)

\(\Rightarrow D\left(1\right)=6\left(\dfrac{12-3b}{2}\right)+9b\)

\(D\left(1\right)=\dfrac{6\left(12-3b\right)}{2}+9b\)

\(D\left(1\right)=3\left(12-3b\right)+9b\)

\(D\left(1\right)=36-9b+9b\)

\(D\left(1\right)=36\)

Vậy: ...

Câu 3:

Sửa đề: \(C=5a-4b+7a-8b\)

\(C=\left(5a+7a\right)-\left(4b+8b\right)\)

\(C=12a-12b\)

\(C=12\left(a-b\right)\)

\(C=12\cdot8\)

\(C=96\)

Vậy: ...

4:

D=6a+9b=3(2a+3b)=36

5: 

D=15a+5b=5(3a+b)=90